设函数f(x)= -ax,g(x)=b
-ax,g(x)=b +2b-1.
+2b-1.
(1)若曲线y=f(x)与y=g(x)在它们的交点(1,c)处有相同的切线,求实数a,b的值;
(2)当a=1,b=0时,求函数h(x)=f(x)+g(x)在区间[t,t+3]内的最小值.
已知函数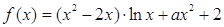 .
.
(1)当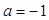 时,求
时,求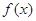 在
在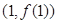 处的切线方程;
处的切线方程;
(2)设函数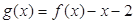 ,
,
(ⅰ)若函数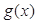 有且仅有一个零点时,求
有且仅有一个零点时,求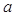 的值;
的值;
(ⅱ)在(ⅰ)的条件下,若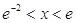 ,
, ,求
,求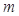 的取值范围。
的取值范围。
已知函数 的图象在
的图象在 处的切线方程为
处的切线方程为 ,其中有e为自然对数的底数。
,其中有e为自然对数的底数。
(1)求 的值;
的值;
(2)当 时,证明
时,证明 ;
;
(3)对于定义域为D的函数 若存在区间
若存在区间 时,使得
时,使得 时,
时, 的值域是
的值域是 。则称
。则称 是该函数
是该函数 的“保值区间”。设
的“保值区间”。设 +
+ ,问函数
,问函数 是否存在“保值区间”?若存在,求出一个“保值区间”,若不存在,说明理由。
是否存在“保值区间”?若存在,求出一个“保值区间”,若不存在,说明理由。
(本小题满分13分)已知函数 .
.
(1)若函数 的图象在
的图象在 处的切线斜率为1,求实数a的值;
处的切线斜率为1,求实数a的值;
(2)若函数 在
在 上是减函数,求实数a的取值范围.
上是减函数,求实数a的取值范围.
已知函数 的图象在点
的图象在点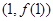 处的切线的斜率为2.
处的切线的斜率为2.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)设 ,讨论
,讨论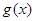 的单调性;
的单调性;
(Ⅲ)已知 且
且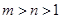 ,证明:
,证明: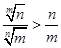
已知函数 ∈R).
∈R).
(1)若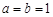 ,求
,求 点(
点(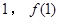 )处的切线方程;
)处的切线方程;
(2)设a≤0,求 的单调区间;
的单调区间;
(3)设a<0,且对任意的 ,
, ≤
≤ ,试比较
,试比较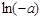 与
与 的大小.
的大小.
已知函数 (m,n为常数,
(m,n为常数,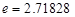 …是自然对数的底数),曲线
…是自然对数的底数),曲线 在点
在点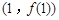 处的切线方程是
处的切线方程是 .
.
(1)求m,n的值;
(2)求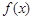 的单调区间;
的单调区间;
(3)设 (其中
(其中 为
为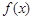 的导函数),证明:对任意
的导函数),证明:对任意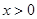 ,
, .
.
己知函数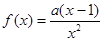 ,其中
,其中
(1)求函数 的单调区间;
的单调区间;
(2)若直线x-y-l=0是曲线y= 的切线,求实数
的切线,求实数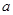 的值;
的值;
(3)设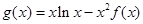 ,求g(x)在区间
,求g(x)在区间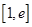 上的最大值(其中e为自然对数的底数)
上的最大值(其中e为自然对数的底数)
(本小题满分14分)设函数 ,
, 且
且 . 曲线
. 曲线 在点
在点 处的切线的斜率为
处的切线的斜率为 .
.
(1)求 的值;
的值;
(2)若存在 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.