高中数学组合几何解答题

（本小题满分12分）已知函数.
（Ⅰ）求函数在点处的切线方程；
（Ⅱ）求过点的函数的切线方程.

已知曲线，求曲线在点处的切线方程．

已知函数图象上一点处的切线方程为．
（1）求的值；
（2）若方程在内有两个不等实根，求的取值范围（其中为自然对数的底数）．

已知函数。
（Ⅰ）若曲线与在公共点处有相同的切线，求实数的值；
（Ⅱ）若，求方程在区间内实根的个数（为自然对数的底数）.

已知函数y=xlnx+1．
（1）求这个函数的导数；
（2）求这个函数的图象在点x=1处的切线方程．

已知曲线 y = x³ + x－2 在点 P₀ 处的切线 平行于直线
4x－y－1=0，且点 P₀ 在第三象限,
⑴求P₀的坐标;
⑵若直线 , 且 l 也过切点P₀ ,求直线l的方程.

若存在过点的直线与曲线和都相切，求的值

求抛物线y＝x²上点到直线x－y－2＝0的最短距离．

某一运动物体，在x(s)时离出发点的距离(单位：m)是f(x)＝x³＋x²＋2x.
(1)求在第1s内的平均速度；
(2)求在1s末的瞬时速度；
(3)经过多少时间该物体的运动速度达到14m/s?

设定义在(0,+∞)上的函数f(x)=ax++b(a>0).
(1)求f(x)的最小值;
(2)若曲线y=f(x)在点(1,f(1))处的切线方程为y=x,求a,b的值.

已知直线y＝kx是曲线y＝ln x的切线，求k.

已知曲线y＝x³＋1，求过点P(1,2)的曲线的切线方程．

已知函数，当时，取得极大值；当时，取得极小值．
求、、的值;
求在处的切线方程．

已知，其中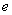是自然常数，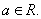
（1）讨论时, 的单调性、极值；
（2）是否存在实数，使的最小值是3，若存在，求出的值；若不存在，说明理由.

已知函数f (x) =
（1）试判断当的大小关系；
（2）试判断曲线和是否存在公切线，若存在，求出公切线方程，若不存在，说明理由；
（3）试比较 (1 + 1×2) (1 + 2×3) ……（1 +2012×2013)与的大小，并写出判断过程．