已知函数f (x) = 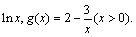
(1)试判断当 的大小关系;
的大小关系;
(2)试判断曲线 和
和 是否存在公切线,若存在,求出公切线方程,若不存在,说明理由;
是否存在公切线,若存在,求出公切线方程,若不存在,说明理由;
(3)试比较 (1 + 1×2) (1 + 2×3) ……(1 +2012×2013)与 的大小,并写出判断过程.
的大小,并写出判断过程.
相关知识点
推荐套卷
已知函数f (x) = 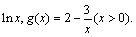
(1)试判断当 的大小关系;
的大小关系;
(2)试判断曲线 和
和 是否存在公切线,若存在,求出公切线方程,若不存在,说明理由;
是否存在公切线,若存在,求出公切线方程,若不存在,说明理由;
(3)试比较 (1 + 1×2) (1 + 2×3) ……(1 +2012×2013)与 的大小,并写出判断过程.
的大小,并写出判断过程.