已知曲线 y = x3 + x－2 在点 P0 处的切线 
平行于直线
4x－y－1=0，且点 P0 在第三象限,
⑴求P0的坐标;
⑵若直线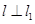 
, 且 l 也过切点P0 ,求直线l的方程.
相关试题
，
，函数
。
的对称中心；
中，
分别是角
的对边，且
，
，且
，求
的值．
,直线
过定点
.
相切，求
、
两点，若
,求此时直线
是公比为
的正项等比数列，
，
。
，求
的前
项和
．
中，
．
，求数列
的通项公式；
成立的
的取值范围．
,椭圆E:
的离心率为
；F是椭圆E的下焦点，直线AF的斜率为
与E 相交于M,N两点，当
的面积最大时，求相关知识点
推荐套卷
已知曲线 y = x3 + x－2 在点 P0 处的切线 平行于直线
4x－y－1=0，且点 P0 在第三象限,
⑴求P0的坐标;
⑵若直线 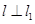, 且 l 也过切点P0 ,求直线l的方程.
粤公网安备 44130202000953号