某一运动物体，在x(s)时离出发点的距离(单位：m)是f(x)＝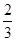
x3＋x2＋2x.
(1)求在第1s内的平均速度；
(2)求在1s末的瞬时速度；
(3)经过多少时间该物体的运动速度达到14m/s?
相关试题
相关知识点
推荐套卷
某一运动物体，在x(s)时离出发点的距离(单位：m)是f(x)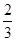＝x3＋x2＋2x.
(1)求在第1s内的平均速度；
(2)求在1s末的瞬时速度；
(3)经过多少时间该物体的运动速度达到14m/s?
粤公网安备 44130202000953号