已知函数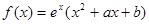 的图象在
的图象在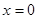 处的切线方程为
处的切线方程为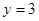 ,其中有e为自然对数的底数。
,其中有e为自然对数的底数。
(1)求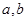 的值;
的值;
(2)当 时,证明
时,证明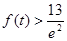 ;
;
(3)对于定义域为D的函数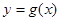 若存在区间
若存在区间 时,使得
时,使得 时,
时,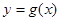 的值域是
的值域是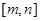 。则称
。则称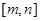 是该函数
是该函数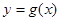 的“保值区间”。设
的“保值区间”。设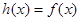 +
+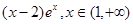 ,问函数
,问函数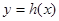 是否存在“保值区间”?若存在,求出一个“保值区间”,若不存在,说明理由。
是否存在“保值区间”?若存在,求出一个“保值区间”,若不存在,说明理由。
相关知识点
推荐套卷
已知函数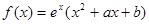 的图象在
的图象在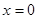 处的切线方程为
处的切线方程为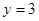 ,其中有e为自然对数的底数。
,其中有e为自然对数的底数。
(1)求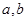 的值;
的值;
(2)当 时,证明
时,证明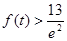 ;
;
(3)对于定义域为D的函数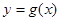 若存在区间
若存在区间 时,使得
时,使得 时,
时,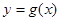 的值域是
的值域是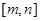 。则称
。则称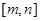 是该函数
是该函数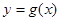 的“保值区间”。设
的“保值区间”。设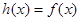 +
+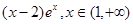 ,问函数
,问函数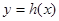 是否存在“保值区间”?若存在,求出一个“保值区间”,若不存在,说明理由。
是否存在“保值区间”?若存在,求出一个“保值区间”,若不存在,说明理由。