已知点O（0，0），A（1，2），B（4，5），且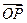
=
＋
．
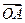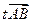（1） 当t变化时，点P是否在一条定直线上运动？
（2） 当t取何值时，点P在y轴上？
（3） OABP能否成为平行四边形？若能求出相应的t值；若不能，请说明理由．
是定义在
上的奇函数，且
，若
时，有
成立.
；
时，
对所有的
恒成立，求实数
的取值范围.
，若
在
上的最大值为
，求
，集合
.
，求
的值；（2）若
，求
，判断
在
上的单调性，并证明.
推荐套卷
已知点O（0，0），A（1，2），B（4，5），且 =＋．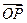
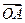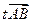（1） 当t变化时，点P是否在一条定直线上运动？
（2） 当t取何值时，点P在y轴上？
（3） OABP能否成为平行四边形？若能求出相应的t值；若不能，请说明理由．
粤公网安备 44130202000953号