高中数学组合几何解答题

已知函数在处取得极值.
(1)求的值;
(2)求函数在上的最小值;
(3)求证:对任意,都有.

已知函数．
（1）讨论函数在定义域内的极值点的个数；
（2）若函数在处取得极值，对,恒成立，求实数的取值范围；
（3）当且时，试比较的大小

已知的图像过原点，且在点处的切线与轴平行，对任意，都有.
(1)求函数在点处切线的斜率；
(2)求的解析式；
(3)设，对任意，都有.求实数的取值范围.

已知函数
(1)当a=2时，求曲线在点处的切线方程;
(2)求函数的极值.

已知函数y=xlnx+1．
（1）求这个函数的导数；
（2）求这个函数的图象在点x=1处的切线方程．

已知函数.
（1）求在点处的切线方程；
（2）求函数在上的最大值.

已知函数.
（1）求在点处的切线方程；
（2）求函数在上的最大值.

（1）已知函数,过点Ｐ的直线与曲线相切，求的方程；
（2）设，当时，在１,４上的最小值为，求在该区间上的最大值．

已知函数（）.
⑴ 若函数的图象在点处的切线的倾斜角为，求在上的最小值；
⑵ 若存在，使，求的取值范围．

已知函数.
（1）若函数的图象在点处的切线的倾斜角为，求在上的最小值；
（2）若存在，使，求a的取值范围．

已知函数在上为增函数，，
（1）求的值；
（2）当时，求函数的单调区间和极值；
（3）若在上至少存在一个，使得成立，求的取值范围.

设函数 $f\left(x\right)=a{e}^x\ln x+\frac{b{e}^{x-1}}{x}$，曲线 $y=f\left(x\right)$在点 $(1,f(1\left)\right)$处的切线方程为 $y=e(x-1)+2$.

（I）求 $a,b$;

（II）证明： $f\left(x\right)>1$.

已知函数，其中，且曲线在点处的切线垂直于.
（1）求的值；
（2）求函数的单调区间与极值.

已知函数（为常数）．
（1）若是函数的一个极值点，求的值；
（2）当时，试判断的单调性；
（3）若对任意的，使不等式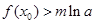恒成立，求实数的取值范围．

已知函数．
（1）若，求曲线在点处的切线方程；
（2）若函数在其定义域内为增函数，求正实数的取值范围；
（3）设函数，若在上至少存在一点，使得＞成立，求实数的取值范围．