已知函数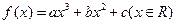 的图象与直线
的图象与直线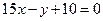 相切于点
相切于点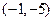 ,且函数
,且函数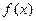 在
在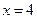 处取得极值。(1)求
处取得极值。(1)求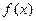 的解析式; (2)求
的解析式; (2)求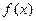 的极值
的极值
已知函数 .
.
(1)求 的导数
的导数 ;
;
(2)求 在闭区间
在闭区间 上的最大值与最小值.
上的最大值与最小值. 
(本 小题满分10分)
小题满分10分)
某工厂要建造一个无 盖长方体水池
盖长方体水池 ,底面一边长固定为8
,底面一边长固定为8 ,
, 最大装水量为72
最大装水量为72 ,池底和池壁的造价分别为
,池底和池壁的造价分别为 元
元 、
、 元
元 ,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?
,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?
(本小题满分14分) 已知函数 在
在 处取得极值。
处取得极值。
(Ⅰ)求函数 的解析式;
的解析式;
( Ⅱ)求证:对于区间
Ⅱ)求证:对于区间 上任意两个自变量的值
上任意两个自变量的值 ,都有
,都有 ;
;
(Ⅲ)若过点 可作曲线
可作曲线 的三条切线,求实数
的三条切线,求实数 的取值范围。
的取值范围。
(本小题满分12分)
已知函数 ,
, 为实数)有极值,且在
为实数)有极值,且在 处的切线与直线
处的切线与直线 平行.
平行.
(I)求实数a的取值范围; (II)是否存在实数a,使得函数
(II)是否存在实数a,使得函数 的极小值为1,若存在,求出实数a的值;若不存
的极小值为1,若存在,求出实数a的值;若不存
在,请说明理由;
(Ⅲ)设
求证: .
.