如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).
(1)求证:平面EFG∥平面PAB;
(2)若点Q是线段PB的中点,求证:PC⊥平面ADQ;
(3)求三棱锥C-EFG的体积.
(本小题满分13分)如图,菱形 的边长为
的边长为 ,现将
,现将 沿对角线
沿对角线 折起至
折起至 位置,并使平面
位置,并使平面 平面
平面 .
. 
(1)求证: ;
;
(2)在菱形 中,若
中,若 ,求直线
,求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)求四面体 体积的最大值.
体积的最大值.
(本小题满分12分)已知正方体 的棱长为
的棱长为 ,
, 分别是棱
分别是棱 的中点,
的中点,
(Ⅰ)求正方体 的内切球的半径与外接球的半径之比;
的内切球的半径与外接球的半径之比;
(Ⅱ)求四棱锥 的体积.
的体积.
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑. 在如图所示的阳马
中,侧棱
底面
,且
,点
是
的中点,连接
.

(Ⅰ)证明:
平面
. 试判断四面体
是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
(Ⅱ)记阳马
的体积为
,四面体
的体积为
,求
的值.
如图1,在直角梯形 中, , 是 的中点, 是 与 的交点,将 沿 折起到图2中 的位置,得到四棱锥 .

(Ⅰ)证明:
平面
;
(Ⅱ)当平面
平面
时,四棱锥
的体积为
,求
的值.
(本小题满分15分)如图,正方形 的边长为1,正方形
的边长为1,正方形 所在平面与平面
所在平面与平面 互相垂直,
互相垂直, 是
是 的中点.
的中点.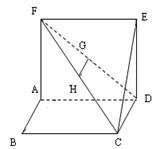
(1)求证: 平面
平面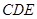 ;
;
(2)求证: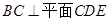 ;
;
(3)求三棱锥 的体积.
的体积.
(本题满分12分,第(1)小题5分,第(2)小题7分)
如图, 是圆柱体
是圆柱体 的一条母线,已知
的一条母线,已知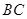 过底面圆的圆心
过底面圆的圆心 ,
, 是圆
是圆 上不与点
上不与点 重合的任意一点,
重合的任意一点, ,
, ,
, .
.
(1)求直线 与直线
与直线 所成角的大小;
所成角的大小;
(2)将四面体 绕母线
绕母线 旋转一周,求
旋转一周,求 的三边在旋转过程中所围成的几何体的体积.
的三边在旋转过程中所围成的几何体的体积.
如图,在四棱锥 中,
中, ,
, 平面
平面 ,
, 平面
平面 ,
, ,
, ,
, .
.
(Ⅰ)求棱锥 的体积;
的体积;
(Ⅱ)求证:平面
 平面
平面 ;
;
(Ⅲ)在线段 上是否存在一点
上是否存在一点 ,使
,使 平面
平面 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(本小题满分12分)已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.
(Ⅰ)若M为CB中点,证明: ;
;
(Ⅱ)求这个几何体的体积.