期中备考总动员高三数学模拟卷【新课标1】4
【改编】在△ABC 中,角A、B、C对应的边为a、b、c,若a、b、c成等比数列,且sinC = 2sinA,则cos B等于 ( )
A. B.
B. C.
C. D.
D.
执行下面的程序框图,若输出的S 值为 ,则框图中的判断框应填入条件是 ( )
,则框图中的判断框应填入条件是 ( )

A. >5 >5 |
B. <5 <5 |
C. ≥5 ≥5 |
D. ≤5 ≤5 |
在如图所示的空间直角坐标系 中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为( )
中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为( )


| A.①和② | B.③和① | C.③和④ | D.④和② |
【改编】下列说法正确的是( )
A.命题“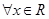 , ,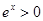 ”的否定是“ ”的否定是“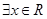 , ,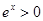 ” ” |
B.命题“已知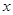 , ,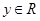 ,若 ,若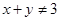 ,则 ,则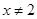 或 或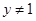 ”的逆否命题是真命题 ”的逆否命题是真命题 |
C.命题“函数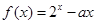 在区间(1,2)有零点充要条件是 在区间(1,2)有零点充要条件是 ” ” |
D.命题“已知命题 、 、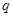 ,若命题 ,若命题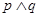 是真命题,则 是真命题,则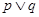 为真命题”的逆命题为真命题 为真命题”的逆命题为真命题 |
【改编】已知数列 是一个单调递增的等差数列,且满足
是一个单调递增的等差数列,且满足 ,
, ,则数列
,则数列 的前2015项和为( )
的前2015项和为( )
A. |
B. |
C. |
D. |
已知抛物线 (
( )与椭圆
)与椭圆 (
( )有相同的焦点
)有相同的焦点 ,点
,点 是两曲线的一个公共点,且
是两曲线的一个公共点,且 轴,则椭圆的离心率为( )
轴,则椭圆的离心率为( )
A. |
B. |
C. |
D. |
【原创】已知函数 ,下列结论中:①函数
,下列结论中:①函数 关于
关于 对称;②函数
对称;②函数 关于(
关于( ,0)对称;③函数
,0)对称;③函数 在(0,
在(0, )是增函数,④将
)是增函数,④将 的图像向右平移
的图像向右平移 可得到
可得到 的图像.其中正确的结论序号为 .
的图像.其中正确的结论序号为 .
【改编】(本小题满分12分)已知数列 的前
的前 项和为
项和为 ,满足
,满足
 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求数列 的前n项和
的前n项和 .
.
(本小题满分12分)已知某校 四个社团的学生人数分别为10,5,20,15.现为了了解社团活动开展情况,用分层抽样的方法从
四个社团的学生人数分别为10,5,20,15.现为了了解社团活动开展情况,用分层抽样的方法从 四个社团的学生当中随机抽取10名学生参加问卷调查.
四个社团的学生当中随机抽取10名学生参加问卷调查.
(Ⅰ)从 四个社团中各抽取多少人?
四个社团中各抽取多少人?
(Ⅱ)在社团 所抽取的学生总数中,任取2个,求
所抽取的学生总数中,任取2个,求 社团中各有1名学生的概率.
社团中各有1名学生的概率.
(本小题满分12分)如图,PA 平面ABCD,四边形ABCD为矩形,PA=AB=
平面ABCD,四边形ABCD为矩形,PA=AB= ,AD=1,点F是PB的中点,点E在边BC上移动.
,AD=1,点F是PB的中点,点E在边BC上移动.
(Ⅰ)当点E为BC的中点时, 证明EF//平面PAC;
(Ⅱ)求三棱锥E-PAD的体积;
(Ⅲ)证明:无论点E在边BC的何处,都有PE AF.
AF.
(本小题满分12分)已知抛物线y2="2px" (p>0)上点T(3,t)到焦点F的距离为4.

(Ⅰ)求t,p的值;
(Ⅱ)设A、B是抛物线上分别位于x轴两侧的两个动点,且  (其中 O为坐标原点).
(其中 O为坐标原点).
(ⅰ)求证:直线AB必过定点,并求出该定点P的坐标;
(ⅱ)过点P作AB的垂线与抛物线交于C、D两点,求四边形ACBD面积的最小值.
(本小题满分12分)已知函数 R
R ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)当 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(本小题满分10分)选修4—5:几何选讲
如图, 为直角三角形,
为直角三角形, ,以AB为直径的圆交AC于点E,点D是BC边的中点,连接OD交圆O于点M,求证:
,以AB为直径的圆交AC于点E,点D是BC边的中点,连接OD交圆O于点M,求证:
(Ⅰ)O、B、D、E四点共圆;
(Ⅱ) .
.
(本小题满分10分)选修4—5:坐标系与参数方程
在直角坐标系 中,半圆C的参数方程为
中,半圆C的参数方程为 (
( 为参数,
为参数, ),以O为极点,x轴的非负半轴为极轴建立极坐标系.
),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求C的极坐标方程;
(Ⅱ)直线 的极坐标方程是
的极坐标方程是 ,射线OM:
,射线OM: 与半圆C的交点为O、P,与直线
与半圆C的交点为O、P,与直线 的交点为Q,求线段PQ的长.
的交点为Q,求线段PQ的长.
 (
( 为虚数单位),则
为虚数单位),则 ( )
( )



 ,则
,则 所含的元素个数为( )
所含的元素个数为( ) 上单调递减的是( )
上单调递减的是( )



 的离心率为2,则椭圆
的离心率为2,则椭圆 的离心率为( )
的离心率为( )



 满足约束条件
满足约束条件 ,若目标函数
,若目标函数 的最大值为12,则
的最大值为12,则 的最小值为( )
的最小值为( )


 分别与曲线
分别与曲线 ,
, 交于A,B,则
交于A,B,则 的最小值为( )
的最小值为( )

 的平均数是
的平均数是 ,标准差是
,标准差是 ,则
,则 __.
__.  中,
中, ,
, ,
, 是
是 的中点,若向量
的中点,若向量 ,且
,且 的终点
的终点 在
在 的内部(不含边界),则
的内部(不含边界),则 的取值范围是 .
的取值范围是 .
 的底面是边长为1的正方形,侧棱长
的底面是边长为1的正方形,侧棱长 ,则异面直线
,则异面直线 与
与 的夹角大小等于
的夹角大小等于 
 .
. 的解集;
的解集; 的不等式
的不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号