（本小题满分12分）已知某校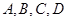
四个社团的学生人数分别为10,5,20,15．现为了了解社团活动开展情况，用分层抽样的方法从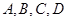四个社团的学生当中随机抽取10名学生参加问卷调查．
（Ⅰ）从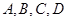四个社团中各抽取多少人？
（Ⅱ）在社团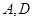
所抽取的学生总数中，任取2个,求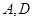社团中各有1名学生的概率．
，α是第三象限角，求sin(195°－α)＋cos(α－15°)的值．
－1)x＋m＝0的两根．
＋
的值．
·
.相关知识点
推荐套卷
（本小题满分12分）已知某校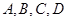四个社团的学生人数分别为10,5,20,15．现为了了解社团活动开展情况，用分层抽样的方法从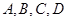四个社团的学生当中随机抽取10名学生参加问卷调查．
（Ⅰ）从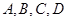四个社团中各抽取多少人？
（Ⅱ）在社团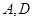所抽取的学生总数中，任取2个,求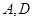社团中各有1名学生的概率．
粤公网安备 44130202000953号