(本小题满分12分)已知抛物线y2="2px" (p>0)上点T(3,t)到焦点F的距离为4.
(Ⅰ)求t,p的值;
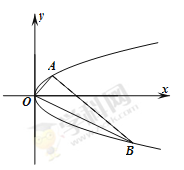
(Ⅱ)设A、B是抛物线上分别位于x轴两侧的两个动点,且 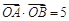 (其中 O为坐标原点).
(其中 O为坐标原点).
(ⅰ)求证:直线AB必过定点,并求出该定点P的坐标;
(ⅱ)过点P作AB的垂线与抛物线交于C、D两点,求四边形ACBD面积的最小值.
相关知识点
推荐套卷
(本小题满分12分)已知抛物线y2="2px" (p>0)上点T(3,t)到焦点F的距离为4.

(Ⅰ)求t,p的值;
(Ⅱ)设A、B是抛物线上分别位于x轴两侧的两个动点,且 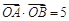 (其中 O为坐标原点).
(其中 O为坐标原点).
(ⅰ)求证:直线AB必过定点,并求出该定点P的坐标;
(ⅱ)过点P作AB的垂线与抛物线交于C、D两点,求四边形ACBD面积的最小值.