(本小题满分12分)如图,在四棱锥P—ABCD中,PA⊥平面ABCD,底面ABCD为梯形,BC∥AD,AB⊥AD,PA=AB=BC=1,AD=2.
(1)求三棱锥P—ACD的外接球的表面积;
(2)若M为PB的中点,问在AD上是否存在一点E,使AM∥平面PCE?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.
如图,在半径为 的半圆形(O为圆心)铁皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上,将所截得的矩形铁皮ABCD卷成一个以AD为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),记圆柱形罐子的体积为
的半圆形(O为圆心)铁皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上,将所截得的矩形铁皮ABCD卷成一个以AD为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),记圆柱形罐子的体积为
 .
.
(1)按下列要求建立函数关系式:
①设 ,将
,将 表示为
表示为 的函数;
的函数;
②设 (
( ),将
),将 表示为
表示为 的函数;
的函数;
(2)请您选用(1)问中的一个函数关系,求圆柱形罐子的最大体积.
如图,在三棱锥 中,
中,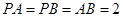 ,
, ,
, °,平面
°,平面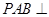 平面
平面 ,
,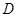 ,
,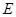 分别为
分别为 ,
,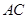 中点.
中点.
(1)求证: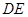 ∥平面
∥平面 ;
;
(2)求证: ;
;
(3)求三棱锥 的体积.
的体积.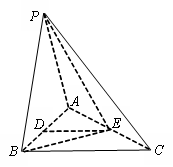
一个几何体是由圆柱ADD1A1和三棱锥E-ABC组合而成,点A,B,C在圆O的圆周上,其正(主)视图,侧(左)视图的面积分别为10和12,如图所示,其中EA⊥平面ABC,AB⊥AC,AB=AC.AE=2.
(1)求证:AC⊥BD.
(2)求三棱锥E-BCD的体积.