北京市东城区高三下学期综合练习二文科试卷
已知一个算法的程序框图如图所示,当输出的结果为0时,输入的 值为( )
值为( )
A. 或 或 |
B. 或 或 |
C. 或 或 |
D. 或 或 |
来源:2014届北京市东城区高三下学期综合练习二文科试卷
对任意实数 ,
, 定义运算“⊙”:
定义运算“⊙”: 设
设 ,若函数
,若函数 的图象与
的图象与 轴恰有三个交点,则
轴恰有三个交点,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
来源:2014届北京市东城区高三下学期综合练习二文科试卷
在棱长为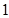 的正方体
的正方体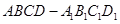 中,点
中,点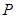 是正方体棱上一点(不包括棱的端点),
是正方体棱上一点(不包括棱的端点),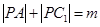 ,
,
①若 ,则满足条件的点
,则满足条件的点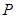 的个数为________;
的个数为________;
②若满足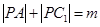 的点
的点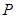 的个数为
的个数为 ,则
,则 的取值范围是________.
的取值范围是________.
来源:2014届北京市东城区高三下学期综合练习二文科试卷
汽车的碳排放量比较大,某地规定,从2014年开始,将对二氧化碳排放量超过130g/km的轻型汽车进行惩罚性征税.检测单位对甲、乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如下(单位:g/km).
经测算得乙品牌轻型汽车二氧化碳排放量的平均值为 .
.
(1)从被检测的5辆甲品牌轻型汽车中任取2辆,则至少有一辆二氧化碳排放量超过 的概率是多少?
的概率是多少?
(2)求表中 的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.
的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.
来源:2014届北京市东城区高三下学期综合练习二文科试卷
如图,在三棱锥 中,
中,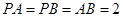 ,
, ,
, °,平面
°,平面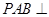 平面
平面 ,
,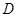 ,
,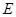 分别为
分别为 ,
,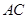 中点.
中点.
(1)求证: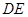 ∥平面
∥平面 ;
;
(2)求证: ;
;
(3)求三棱锥 的体积.
的体积.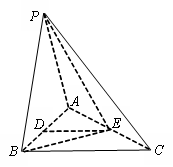
来源:2014届北京市东城区高三下学期综合练习二文科试卷
已知 ,函数
,函数 ,
, .
.
(Ⅰ)若曲线 与曲线
与曲线 在它们的交点
在它们的交点 处的切线互相垂直,求
处的切线互相垂直,求 ,
, 的值;
的值;
(Ⅱ)设 ,若对任意的
,若对任意的 ,且
,且 ,都有
,都有 ,求
,求 的取值范围.
的取值范围.
来源:2014届北京市东城区高三下学期综合练习二文科试卷
已知椭圆 的一个焦点为
的一个焦点为 ,且离心率为
,且离心率为 .
.
(1)求椭圆方程;
(2)过点 且斜率为
且斜率为 的直线与椭圆交于
的直线与椭圆交于 两点,点
两点,点 关于
关于 轴的对称点为
轴的对称点为 ,求△
,求△ 面积的最大值.
面积的最大值.
来源:2014届北京市东城区高三下学期综合练习二文科试卷
 ,集合
,集合 ,则
,则 =( )
=( )



 对应的点位于( )
对应的点位于( ) 的前
的前 项和为
项和为 ,若
,若 ,则
,则 的值是( )
的值是( )



 ,那么
,那么 的值是( )
的值是( )



 在[0,+∞]上是增函数,
在[0,+∞]上是增函数, ,若
,若 则
则 的取值范围是( )
的取值范围是( )



 ,
, ,
, ,若线段
,若线段 和
和 有相同的垂直平分线,则点
有相同的垂直平分线,则点 的坐标是( )
的坐标是( )



 的定义域是 .
的定义域是 . ,
, ,且
,且 ∥
∥ ,则
,则 .
. 上随机取两个实数
上随机取两个实数 ,
, ,则事件“
,则事件“ ”的概率为_________.
”的概率为_________.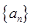 的前
的前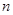 项和为
项和为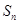 ,且对任意
,且对任意 ,有
,有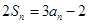 ,则
,则 ;
; .
. 且斜率为
且斜率为 的直线与抛物线
的直线与抛物线 相交于
相交于 ,
, 两点,若
两点,若 中点,则
中点,则 的值是 .
的值是 . .
. 的值;
的值; 时,求函数
时,求函数 的最大值和最小值.
的最大值和最小值.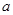 是一个自然数,
是一个自然数, 是
是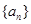 :
: 是自然数,
是自然数,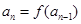 (
( ,
, ).
). ,
,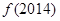 ;
; ,求证:
,求证: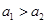 ;
; ,使得
,使得 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号