《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑. 在如图所示的阳马
中,侧棱
底面
,且
,点
是
的中点,连接
.
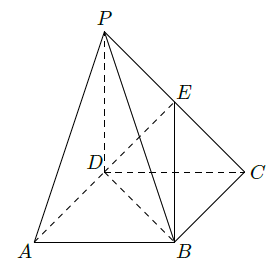
(Ⅰ)证明:
平面
. 试判断四面体
是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
(Ⅱ)记阳马
的体积为
,四面体
的体积为
,求
的值.
相关知识点
推荐套卷
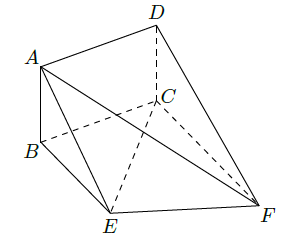
 (1)试确定E点位置;
(1)试确定E点位置; ,AB=
,AB= ,AC=2,A1C1=1,
,AC=2,A1C1=1, =
= .
.

 (1)直线EF∥平面ACD;
(1)直线EF∥平面ACD; 粤公网安备 44130202000953号
粤公网安备 44130202000953号