如图,在三棱锥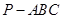 中,
中,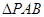 和
和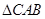 都是以
都是以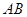 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,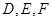 分别是
分别是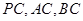 的中点.
的中点.
(1)证明:平面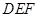 //平面
//平面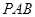 ;
;
(2)证明: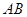
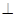
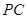 ;
;
(3)若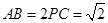 ,求三棱锥
,求三棱锥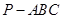 的体积.
的体积.
如图,在边长为4的菱形ABCD中,∠DAB=60°,点E、F分别在边CD、CB上,点E与点C、D不重合,EF⊥AC,EF∩AC=O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABFED.
(1)求证:BD⊥平面POA;
(2)记三棱锥PABD体积为V1,四棱锥PBDEF体积为V2,且 ,求此时线段PO的长.
,求此时线段PO的长.
如图a,在直角梯形ABCD中,AB⊥AD,AD∥BC,F为AD的中点,E在BC上,且EF∥AB.已知AB=AD=CE=2,沿线EF把四边形CDFE折起如图b,使平面CDFE⊥平面ABEF.
(1)求证:AB⊥平面BCE;
(2)求三棱锥C ADE体积.
在等腰梯形ABCD中,AB∥CD,AB=BC=AD=2,CD=4,E为边DC的中点,如图1.将△ADE沿AE折起到△AEP位置,连PB、PC,点Q是棱AE的中点,点M在棱PC上,如图2.
(1)若PA∥平面MQB,求PM∶MC;
(2)若平面AEP⊥平面ABCE,点M是PC的中点,求三棱锥AMQB的体积.
在直三棱柱 中,
中, 分别是
分别是 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求多面体 的体积.
的体积.
在直角梯形ABCD中,AB∥CD,AD⊥AB,CD=2AB=4,AD= ,E为CD的中点,将△BCE沿BE折起,使得CO⊥DE,其中垂足O在线段DE内.
,E为CD的中点,将△BCE沿BE折起,使得CO⊥DE,其中垂足O在线段DE内.
(1)求证:CO⊥平面ABED;
(2)问∠CEO(记为θ)多大时,三棱锥C-AOE的体积最大,最大值为多少.
有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.
如图所示为一个几何体的直观图、三视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形).
(1)求四棱锥P-ABCD的体积;
(2)若G为BC上的动点,求证:AE⊥PG.
如图,四边形ABCD是边长为2的正方形,直线l与平面ABCD平行,E和F是l上的两个不同点,且EA=ED,FB=FC.E′和F′是平面ABCD内的两点,EE′和FF′都与平面ABCD垂直.
(1)证明:直线E′F′垂直且平分线段AD;
(2)若∠EAD=∠EAB=60 °,EF=2.求多面体ABCDEF的体积.
已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.
(1)求该几何体的体积V;
(2)求该几何体的侧面积S.
如图,在三棱柱ABC-A1B1C1中,C1C⊥底面ABC,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.
(1)求证:AC1∥平面CDB1;
(2)求三棱锥D-B1C1C的体积.
如图,在三棱柱ABC-A1B1C1中,C1C⊥底面ABC,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.
(1)求证:AC1∥平面CDB1;
(2)求四面体B1C1CD的体积.
下图是一几何体的直观图、主视图、俯视图、左视图.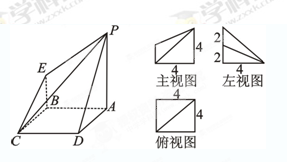
(1)若F为PD的中点,求证:AF⊥面PCD;
(2)证明:BD∥面PEC;
(3)求该几何体的体积.
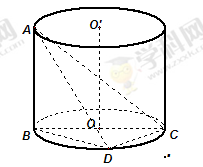
如图, 是圆柱体
是圆柱体 的一条母线,
的一条母线,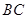 过底面圆的圆心
过底面圆的圆心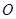 ,
,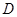 是圆
是圆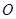 上不与点
上不与点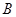 、
、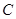 重合的任意一点,已知棱
重合的任意一点,已知棱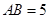 ,
, ,
,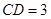 .
.
(1)求证: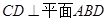 ;
;
(2)将四面体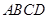 绕母线
绕母线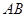 转动一周,求
转动一周,求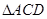 的三边在旋转过程中所围成的几何体的体积.
的三边在旋转过程中所围成的几何体的体积.