在直角梯形ABCD中，AB∥CD，AD⊥AB，CD＝2AB＝4，AD＝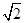
，E为CD的中点，将△BCE沿BE折起，使得CO⊥DE，其中垂足O在线段DE内．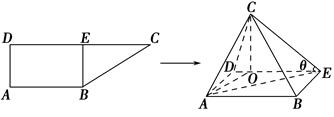
(1)求证：CO⊥平面ABED；
(2)问∠CEO(记为θ)多大时，三棱锥C－AOE的体积最大，最大值为多少．
相关试题
，
（
）
时，函数
在其定义域是增函数，求b的取值范围。
，
，求函数
的最小值
在
上的单调性，并给出证明；
Í
与
的单调递增区间与对称轴方程，对称中心坐标；
时，求函数
,求实数
的值;
,求实数
使得
,试求
的最小值．
；
是定值相关知识点
推荐套卷
在直角梯形ABCD中，AB∥CD，AD⊥AB，CD＝2AB＝4，AD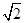＝，E为CD的中点，将△BCE沿BE折起，使得CO⊥DE，其中垂足O在线段DE内．
(1)求证：CO⊥平面ABED；
(2)问∠CEO(记为θ)多大时，三棱锥C－AOE的体积最大，最大值为多少．
粤公网安备 44130202000953号