如图,已知圆锥的底面半径为 ,点Q为半圆弧
,点Q为半圆弧 的中点,点
的中点,点 为母线
为母线 的中点.若直线
的中点.若直线 与
与 所成的角为
所成的角为 ,求此圆锥的表面积.
,求此圆锥的表面积.
若三角形内切圆半径为 ,三边长分别为
,三边长分别为 ,则三角形的面积为
,则三角形的面积为 ,根据类比思想,若四面体内切球半径为
,根据类比思想,若四面体内切球半径为 ,四个面的面积分别为
,四个面的面积分别为 ,则这个四面体的体积为( )
,则这个四面体的体积为( )
A. |
B. |
C. |
D. |
)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
(Ⅰ)求证:平面DAF⊥平面CBF;
(Ⅱ)设FC的中点为M,求证:OM∥平面DAF;
(Ⅲ)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为 ,求
,求 .
.
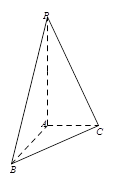
(本小题满分12分)如图,在三棱锥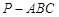 中,
中, 丄平面
丄平面 ,
,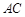 丄
丄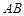 ,
, ,
, .
.
(Ⅰ)证明: 丄
丄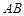 ;
;
(Ⅱ)求二面角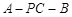 的正弦值;
的正弦值;
(Ⅲ)求三棱锥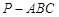 外接球的体积.
外接球的体积.
三棱锥 中,
中, 平面
平面 ,
, 为侧棱
为侧棱 上一点,它的正视图和侧视图 (如下图所示),则
上一点,它的正视图和侧视图 (如下图所示),则 与平面
与平面 所成角的大小为__ _;三棱锥
所成角的大小为__ _;三棱锥 的体积为 __ _.
的体积为 __ _.
(本小题满分12分)如图,四棱锥 的底面是边长为1的正方形,
的底面是边长为1的正方形, ,
, ,
, 为
为 的中点,
的中点, 为
为 上一点,且
上一点,且 .
.
(1)证明: 平面
平面 ;
;
(2)证明: 平面
平面 ;
;
(3)求三棱锥 的体积.
的体积.
如图,在直三棱柱ABCA1B1C1中,AB=AC=5,BB1=BC=6,D,E分别是AA1和B1C的中点.
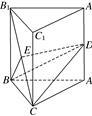
(1)求证:DE∥平面ABC;
(2)求三棱锥EBCD的体积.
如图,在三棱锥 中,平面
中,平面 平面
平面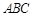 ,
, 为等边三角形,
为等边三角形, ,且
,且 ,O,M分别为
,O,M分别为 ,
, 的中点.
的中点.
(Ⅰ)求证: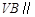 平面
平面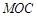 ;
;
(Ⅱ)设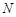 是线段
是线段 上一点,满足平面
上一点,满足平面 平面
平面 ,试说明点的位置
,试说明点的位置 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
如图,已知 平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,
平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形, ,
, ,
, ,
, .
.
(1)求证: 平面BCE;
平面BCE;
(2)求证: 平面BCE;
平面BCE;
(3)求三棱锥 的体积.
的体积.
在如图所示的几何体中,四边形ABCD是正方形,MA⊥平面ABCD,PD∥MA,E、G、F分别为MB、PB、PC的中点,且AD=PD=2MA.
(1)求证:平面EFG∥平面PMA;
(2)求证:平面EFG⊥平面PDC;
(3)求三棱锥P-MAB与四棱锥P-ABCD的体积之比.