江西省抚州市七校高一下学期期末联考数学试卷
已知直线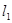 经过
经过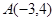 ,
, 两点,直线
两点,直线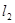 倾斜角为
倾斜角为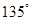 ,那么
,那么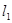 与
与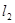 ( )
( )
| A.垂直 | B.平行 | C.重合 | D.相交但不垂直 |
设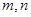 表示两条不同直线,,
表示两条不同直线,, 表示三个不同的平面,有以下四个结论:
表示三个不同的平面,有以下四个结论:
①若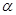 ∥
∥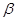 ,
,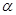 ∥
∥ ,则
,则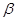 ∥
∥
② 若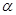
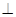
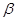 ,
,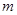 ∥
∥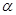 ,则
,则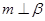
③若 ,
,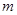 ∥
∥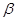 ,则
,则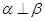
④若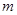 ∥
∥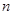 ,
,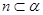 ,则
,则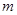 ∥
∥
其中正确的序号( )
| A.①③ | B.①④ | C.②③ | D.②④ |
如果一个几何体的三视图如图所示(单位长度: cm),则此几何体的表面积是( )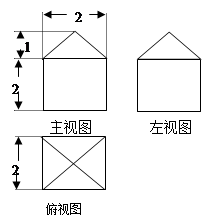
A.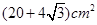 |
B.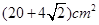 |
C.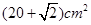 |
D.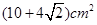 |
已知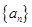 为等差数列,
为等差数列,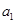 +
+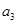 +
+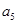 =105,
=105,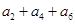 =99,以
=99,以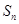 表示
表示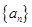 的前
的前 项和,则使得
项和,则使得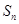 达到最大值的
达到最大值的 是( )
是( )
| A.21 | B.20 | C.19 | D.18 |
已知直线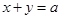 与圆
与圆 交于
交于 两点,
两点,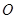 是坐标原点,向量
是坐标原点,向量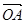 、
、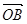 满足
满足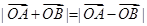 ,则实数a的值是( )
,则实数a的值是( )
| A.2 | B.-2 | C.2或-2 | D.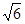 或- 或-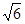 |
如图,用一边长为 的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为
的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为 的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋最高点与蛋巢底面的距离为 ( )
的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋最高点与蛋巢底面的距离为 ( ) 
A. |
B. |
C. |
D. |
若 是函数
是函数 的两个不同的零点,且
的两个不同的零点,且 这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则
这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则 的值等于________
的值等于________
如图所示,正方体 的棱长为1,
的棱长为1, 分别是棱
分别是棱 ,
, 的中点,过直线
的中点,过直线 的平面分别与棱
的平面分别与棱 、
、 分别交于
分别交于 两点,设
两点,设 ,
, ,给出以下四个结论:
,给出以下四个结论:
①平面
 平面
平面 ;
;
②直线 ∥平面
∥平面 始终成立;
始终成立;
③四边形 周长
周长 ,
, 是单调函数;
是单调函数;
④四棱锥 的体积
的体积 为常数;
为常数;
以上结论正确的是___________.
(本小题10分).已知公差不为零的等差数列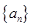 中,
中, ,且
,且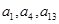 成等比数列.
成等比数列.
(Ⅰ)求数列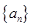 的通项公式;
的通项公式;
(Ⅱ)令 (
(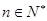 ),求数列
),求数列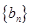 的前
的前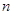 项和
项和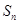 .
.
(本小题12分).如图,矩形 的顶点
的顶点 为原点,
为原点, 边所在直线的方程为
边所在直线的方程为 ,顶点
,顶点 的纵坐标为
的纵坐标为 .
.
(1)求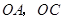 边所在直线的方程;
边所在直线的方程;
(2)求矩形 的面积.
的面积.
(本小题满分12分)已知函数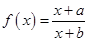 (
(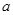 、
、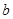 为常数).
为常数).
(1)若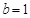 ,解不等式
,解不等式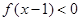 ;
;
(2)若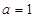 ,当
,当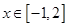 时,
时,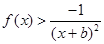 恒成立,求
恒成立,求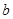 的取值范围.
的取值范围.
(本小题满分12分)如图,四棱锥 的底面是边长为1的正方形,
的底面是边长为1的正方形, ,
, ,
, 为
为 的中点,
的中点, 为
为 上一点,且
上一点,且 .
.
(1)证明: 平面
平面 ;
;
(2)证明: 平面
平面 ;
;
(3)求三棱锥 的体积.
的体积.
(本小题满分12分)如图,在平面直角坐标系内,已知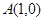 ,
,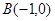 两点,且圆
两点,且圆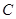
的方程为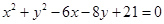 ,点
,点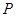 为圆
为圆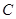 上的动点.
上的动点.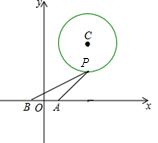
(1)求过点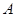 的圆的切线的方程;
的圆的切线的方程;
(2)求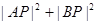 的最大值及其对应的点
的最大值及其对应的点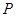 的坐标.
的坐标.
 ,则
,则

 ,则
,则
 ,则
,则
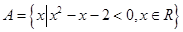 ,
,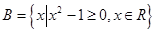 ,则
,则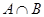 =( )
=( )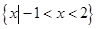
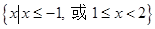
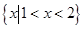
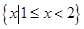
 关于直线
关于直线 对称的直线方程是( )
对称的直线方程是( )



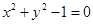 和
和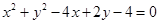 的位置关系是( )
的位置关系是( ) 满足
满足 ,则
,则 的最小值为( )
的最小值为( )

 中,
中, ,
, ,
, 是
是 的个位数字,
的个位数字, 是
是 的前
的前 项和,则
项和,则 ( )
( )



 中,
中, ,
,
 是
是 与
与 的交点,则
的交点,则
 ,且
,且 ,则
,则 的最小值等于_______.
的最小值等于_______. 的前
的前 项和为
项和为 ,已知
,已知
 与
与 之间插入
之间插入 个数组成一个公差为
个数组成一个公差为 的等差数列,
的等差数列, ,
, ,
, (其中
(其中 成等差数列)成等比数列?若存在,求出这样的三项,若不存在,说明理由;
成等差数列)成等比数列?若存在,求出这样的三项,若不存在,说明理由; ,求满足
,求满足 的
的 粤公网安备 44130202000953号
粤公网安备 44130202000953号