已知直三棱柱 中,
中, ,侧面
,侧面 的面积为
的面积为 ,则直三棱柱
,则直三棱柱 外接球表面积的最小值为 .
外接球表面积的最小值为 .
如图:已知四棱柱 的底面是菱形,该菱形的边长为1,
的底面是菱形,该菱形的边长为1, ,
, .
.
(1)设棱形 的对角线的交点为
的对角线的交点为 ,求证:
,求证: //平面
//平面 ;
;
(2)若四棱柱的体积 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)如图,矩形 中,对角线
中,对角线 的交点为
的交点为 ⊥平面
⊥平面
 为
为 上的点,且
上的点,且 .
.
(I)求证: ⊥平面
⊥平面 ;
;
(II)求三棱锥 的体积.
的体积.
如图,在三棱锥P﹣ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.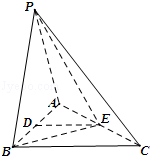
(Ⅰ)求证:DE∥面PBC;
(Ⅱ)求证:AB⊥PE;
(Ⅲ)求三棱锥B﹣PEC的体积.
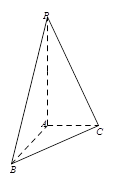
(本小题满分12分)如图,在三棱锥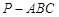 中,
中, 丄平面
丄平面 ,
,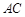 丄
丄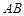 ,
, ,
, .
.
(Ⅰ)证明: 丄
丄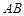 ;
;
(Ⅱ)求二面角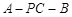 的正弦值;
的正弦值;
(Ⅲ)求三棱锥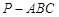 外接球的体积.
外接球的体积.
如图,在直三棱柱ABCA1B1C1中,AB=AC=5,BB1=BC=6,D,E分别是AA1和B1C的中点.
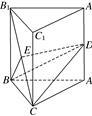
(1)求证:DE∥平面ABC;
(2)求三棱锥EBCD的体积.
如图,在三棱锥 中,平面
中,平面 平面
平面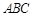 ,
, 为等边三角形,
为等边三角形, ,且
,且 ,O,M分别为
,O,M分别为 ,
, 的中点.
的中点.
(Ⅰ)求证: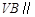 平面
平面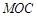 ;
;
(Ⅱ)设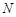 是线段
是线段 上一点,满足平面
上一点,满足平面 平面
平面 ,试说明点的位置
,试说明点的位置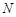 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
如图,已知 平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,
平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形, ,
, ,
, ,
, .
.
(1)求证: 平面BCE;
平面BCE;
(2)求证: 平面BCE;
平面BCE;
(3)求三棱锥 的体积.
的体积.