广东省广州市荔湾区高三上学期调研测试一理科数学试卷
椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,离心率等于
轴上,离心率等于 ,且它的一个顶点恰好是抛物线
,且它的一个顶点恰好是抛物线
的焦点,则椭圆 的标准方程为
的标准方程为
A. |
B. |
C. |
D. |
将函数 的图象向左平移
的图象向左平移 个单位后的图形关于原点对称,则函数
个单位后的图形关于原点对称,则函数 在
在 上的最小值为
上的最小值为
A. |
B. |
C. |
D. |
已知不等式组 所表示的平面区域为
所表示的平面区域为 ,若直线
,若直线 与平面区域
与平面区域 有公共点,
有公共点,
则 的取值范围为是
的取值范围为是
A. |
B. |
C. |
D. |
某几何体的三视图如图所示,图中的四边形都是边长为 的正方形,两条虚线互相垂直,则该几何体的体积是
的正方形,两条虚线互相垂直,则该几何体的体积是
A. |
B. |
C. |
D. |
如图, 、
、 是双曲线
是双曲线 的左、右焦点,过
的左、右焦点,过 的直线
的直线 与双曲线的左
与双曲线的左
右两支分别交于点 、
、 .若
.若 为等边三角形,则双曲线的离心率为
为等边三角形,则双曲线的离心率为
| A.4 | B. |
C. |
D. |
(本小题满分12分)已知数列 满足:
满足: ,
, ,
, ,(
,( ).
).
(1)求证: 是等差数列,并求出
是等差数列,并求出 ;
;
(2)证明: .
.
(本小题满分12分)如图,矩形 所在的平面与等边
所在的平面与等边 所在的平面垂直,
所在的平面垂直, ,
, 为
为 的中点.
的中点.
(1)求证: ;
;
(2)求二面角 的余弦值.
的余弦值.
(本小题满分12分)某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的
统计结果如下:
| 日销售量(吨) |
1 |
1.5 |
2 |
| 频数 |
10 |
25 |
15 |
| 频率 |
0.2 |
 |
 |
(1)求表中的 的值;
的值;
(2)若以上表频率作为概率,且每天的销售量相互独立.求:
①5天中该种商品恰好有2天的销售量为1.5吨的概率;
②已知每吨该商品的销售利润为2千元, 表示该种商品两天销售利润的和(单位:千元)求
表示该种商品两天销售利润的和(单位:千元)求 的分布列和期望.
的分布列和期望.
(本小题满分12分)已知椭圆C:  的离心率为
的离心率为 ,且过点(1,
,且过点(1, ).
).
(1)求椭圆C的方程;
(2)设与圆 相切的直线
相切的直线 交椭圆C与A,B两点,求
交椭圆C与A,B两点,求 面积的最大值,及取得最大值时直线
面积的最大值,及取得最大值时直线 的方程.
的方程.
(本小题满分12分)已知函数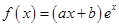 (
(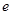 为自然对数的底数),曲线
为自然对数的底数),曲线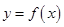 在点
在点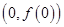 处的切线方程为
处的切线方程为 .
.
(1)求 ,
, 的值;
的值;
(2)任意 ,
, 时,证明:
时,证明: .
.
(本小题满分10分)选修4-1:几何证明选讲
如图, 是⊙
是⊙ 的直径,
的直径, 是弧
是弧 的中点,
的中点, ,垂足为
,垂足为 ,
, 交
交 于点
于点 .
.
(1)求证: ;
;
(2)若 ,⊙
,⊙ 的半径为6,求
的半径为6,求 的长.
的长.
(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 ,(
,( 为参数),以原点
为参数),以原点 为极点,
为极点, 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.
(1)求曲线 的普通方程与曲线
的普通方程与曲线 的直角坐标方程;
的直角坐标方程;
(2)设 为曲线
为曲线 上的动点,求点
上的动点,求点 到
到 上点的距离的最小值.
上点的距离的最小值.
 ,
, ,则
,则




 是虚数单位,若复数
是虚数单位,若复数 满足
满足 ,则复数
,则复数




 中,
中,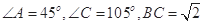 , 则边长
, 则边长 为
为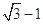

 的值是
的值是




 的图像大致为
的图像大致为
 的展开式中
的展开式中 的系数是
的系数是 ,则方程
,则方程 恰有两个不同的实根时,实数
恰有两个不同的实根时,实数 的取值范围是
的取值范围是



 ,
, ,则
,则 .
. 中,
中,
 .点
.点 满足
满足 ,则
,则 ______,
______, 中任取一点,则该点落在阴影部分中的概率为 .
中任取一点,则该点落在阴影部分中的概率为 .
 中,
中, ,侧面
,侧面 的面积为
的面积为 ,则直三棱柱
,则直三棱柱 .
. ;
; 对一切实数
对一切实数 均成立,求
均成立,求 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号