广东省惠州市高三第一次调研考试数学文试卷
已知流程图如图所示,该程序运行后,为使输出的 值为16,则循环体的判断框内①处应填 ( )
值为16,则循环体的判断框内①处应填 ( )

A. |
B. |
C. |
D. |
来源:2016届广东省惠州市高三第一次调研考试数学文试卷
对函数 ,在使
,在使 成立的所有常数
成立的所有常数 中,我们把
中,我们把 的最大值叫做函数
的最大值叫做函数 的下确界.现已知定义在R上的偶函数
的下确界.现已知定义在R上的偶函数 满足
满足 ,当
,当 时,
时, ,则
,则 的下确界为 ( )
的下确界为 ( )
A. |
B. |
C. |
D. |
来源:2016届广东省惠州市高三第一次调研考试数学文试卷
(本小题满分12分)
已知 为等差数列,且满足
为等差数列,且满足 .
.
(I)求数列 的通项公式;
的通项公式;
(II)记 的前
的前 项和为
项和为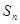 ,若
,若 成等比数列,求正整数
成等比数列,求正整数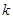 的值.
的值.
来源:2016届广东省惠州市高三第一次调研考试数学文试卷
(本小题满分12分)某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.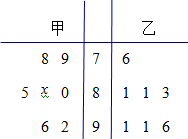
(I)计算甲班7位学生成绩的方差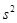 ;
;
(II)从成绩在90分以上的学生中随机抽取两名学生,求甲班至少有一名学生的概率.
参考公式:
方差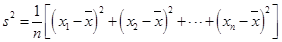 ,其中
,其中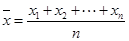 .
.
来源:2016届广东省惠州市高三第一次调研考试数学文试卷
(本小题满分12分)如图,矩形 中,对角线
中,对角线 的交点为
的交点为 ⊥平面
⊥平面
 为
为 上的点,且
上的点,且 .
.
(I)求证: ⊥平面
⊥平面 ;
;
(II)求三棱锥 的体积.
的体积.
来源:2016届广东省惠州市高三第一次调研考试数学文试卷
(本小题满分12分)在平面直角坐标系 中,已知圆心在
中,已知圆心在 轴上,半径为4的圆
轴上,半径为4的圆 位于
位于 轴右侧,且与
轴右侧,且与 轴相切.
轴相切.
(I)求圆 的方程;
的方程;
(II)若椭圆 的离心率为
的离心率为 ,且左右焦点为
,且左右焦点为 .试探究在圆
.试探究在圆 上是否存在点
上是否存在点 ,使得
,使得 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
来源:2016届广东省惠州市高三第一次调研考试数学文试卷
(本小题满分12分)已知函数 .
.
(I)讨论函数 的单调区间;
的单调区间;
(II)当 时,若函数
时,若函数 在区间
在区间 上的最大值为
上的最大值为 ,求
,求 的取值范围.
的取值范围.
来源:2016届广东省惠州市高三第一次调研考试数学文试卷
(本小题满分10分 )选修4—1:几何证明选讲
如图, 为⊙
为⊙ 的直径,直线
的直径,直线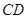 与⊙
与⊙ 相切于点
相切于点 ,
,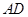 垂直
垂直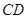 于点
于点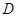 ,
,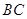 垂直
垂直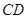 于点
于点 ,
,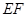 垂直
垂直 于点
于点 ,连接
,连接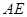 ,
, .
.
证明:(Ⅰ)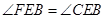 ;
;
(Ⅱ)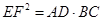 .
.
来源:2016届广东省惠州市高三第一次调研考试数学文试卷
(本小题满分10分 )选修4—4:坐标系与参数方程
在直角坐标系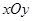 中,直线
中,直线 的参数方程为
的参数方程为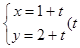 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点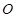 为极点,
为极点,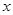 轴的正半轴为极轴的极坐标系下,圆
轴的正半轴为极轴的极坐标系下,圆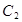 的方程为
的方程为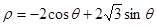 .
.
(Ⅰ)求直线 的普通方程和圆
的普通方程和圆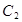 的圆心的极坐标;
的圆心的极坐标;
(Ⅱ)设直线 和圆
和圆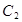 的交点为
的交点为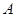 、
、 ,求弦
,求弦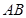 的长.
的长.
来源:2016届广东省惠州市高三第一次调研考试数学文试卷
 ,则
,则 等于 ( )
等于 ( )



 的焦距为( )
的焦距为( )



 (
( 是虚数单位),则
是虚数单位),则 ( )
( )



 ( )
( )



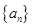 中,若
中,若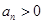 且
且 ,则
,则 的值为 ( )
的值为 ( ) 的图象中相邻的两条对称轴间距离为 ( )
的图象中相邻的两条对称轴间距离为 ( )



 、
、 ,下列结论中,正确的是( )
,下列结论中,正确的是( )








 ,且
,且 ,则
,则 ( )
( ) 的焦点
的焦点 作直线交抛物线于
作直线交抛物线于 、
、 两点,如果
两点,如果 ,那么
,那么 = ( )
= ( )



 ,则
,则 .
. 有实根的概率为 .
有实根的概率为 . 的坐标满足条件
的坐标满足条件 点
点 为坐标原点,那么
为坐标原点,那么 的最大值等于 .
的最大值等于 . (
(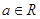 ,
, 为自然对数的底数),若函数
为自然对数的底数),若函数 在点
在点 处的切线平行于
处的切线平行于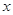 轴,则
轴,则 .
.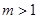 ,且关于
,且关于 的不等式
的不等式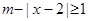 的解集为
的解集为 .
. 的值;
的值; ,
, 均为正实数,且满足
均为正实数,且满足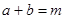 ,求
,求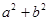 的最小值.
的最小值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号