高中数学多面角及多面角的性质试题

已知函数 $f\left(x\right)={\sin }^{2}x+a\sin x\cos x-{\cos }^{2}x$，且 $f\left(\frac{\mathrm{\pi }}{4}\right)=1$.

（1）求常数a的值及 $f\left(x\right)$的最小值；
（2）当 $x\in \left[0,\frac{\mathrm{\pi }}{2}\right]$时，求 $f\left(x\right)$的单调增区间．

已知函数，钝角（角对边为）的角满足.
（1）求函数的单调递增区间；
（2）若，求.

已知函数，其中为常数．
（1）求函数的周期；
（2）如果的最小值为，求的值，并求此时的最大值及图像的对称轴方程.

已知向量，，且．
（1）将表示为的函数，并求的单调递增区间；
（2）已知分别为的三个内角对应的边长，若，且，，求的面积．

已知函数的周期为，图象的一个对称中心为，将函数图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将得到的图象向右平移个单位长度后得到函数的图象。
（1）求函数与的解析式
（2）是否存在，使得按照某种顺序成等差数列？若存在，请确定的个数，若不存在，说明理由；
（3）求实数与正整数，使得在内恰有2013个零点

已知函数，下列结论中错误的是（  ）

A．的图像关于点中心对称

B．的图像关于直线对称

C．的最大值为

D．既是奇函数，又是周期函数

设，，，,则的大小关系是（　　）

A．

B．

C．

D．

若动直线与函数和的图像分别交于两点，则的最大值为（   ）

A．1

B．

C．

D．2

已知函数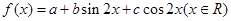的图像过点，且b>0，又的最大值为.
（Ⅰ）将写成含的形式；
（Ⅱ）由函数y =图像经过平移是否能得到一个奇函数y =的图像？若能，请写出平移的过程；若不能，请说明理由。

已知函数的部分图象如图所示，是图象的最高点，为图象与轴的交点，为坐标原点，若

（1）求函数的解析式，
（2）将函数的图象向右平移2个单位后得到函数的图象，当时，求函数的值域．

（本小题满分12分）已知函数）．
（1）求函数的最小正周期；
（2）若，求的值．

已知函数的周期为 ，图像的一个对称中心为，将函数图像上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将所得到的图像向右平移个单位长度后得到函数的图像．
（1）求函数与的解析式；
（2）若 ，是第一象限的角，且 ，求 的值．

已知函数（其中为常数，且）的部分图像如图所示．

（1）求函数的解析式
（2）若求的值

（本小题满分10分）已知函数，且当时，的最小值为2，
（1）求的单调递增区间；
（2）先将函数的图象上的点纵坐标不变，横坐标缩小到原来的，再把所得的图象向右平移个单位，得到函数的图象，求方程在区间上所有根之和．

已知函数，且给定条件p：“”，
（1）求f（x）的最大值及最小值
（2）若又给条件q：“|f（x）﹣m|＜2“且p是q的充分条件，求实数m的取值范围．