高中数学多面角及多面角的性质试题

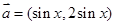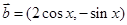已知向量，，函数．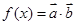
（1）求函数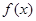的最小正周期；
（2）求函数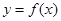在上的值域．

（本小题满分12分）根据下列算法语句，将输出的A值依次记为

（Ⅰ）求数列的通项公式；
（Ⅱ）已知函数的最小正周期是，且函数的图象关于直线对称，求函数在区间上的值域．

已知函数（其中为常数，且）的部分图像如图所示．

（1）求函数的解析式
（2）若求的值

若函数，且，的最小值是，则的单调递增区间是（   ）

A．

B．

C．

D．

函数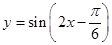的图像与函数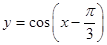的图像（   ）

A．有相同的对称轴但无相同的对称中心

B．有相同的对称中心但无相同的对称轴

C．既有相同的对称轴也有相同的对称中心

D．既无相同的对称中心也无相同的对称轴

（本小题满分12分）已知函数．
（Ⅰ）求函数的最小正周期及在区间上的最大值和最小值；
（Ⅱ）将函数图像向左平移个单位，再向上平移个单位，得到函数图像，求的对称轴方程和对称中心坐标．

如图，在平面直角坐标系中，，，．

（1）求的面积；
（2）若函数的图象经过、、三点，且、为的图象与轴相邻的两个交点，求的解析式．

下列对于函数 的判断正确的是 （   ）

A．函数的周期为

B．对于函数都不可能为偶函数

C．,使

D．函数在区间内单调递增

已知函数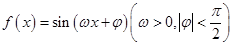的部分图象如图所示．

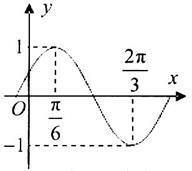
（1）求函数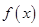的解析式，并写出 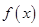的单调递减区间；
（2）已知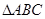的内角分别是A，B，C，角A为锐角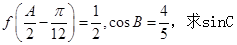，的值．

设满足约束条件，若目标函数的最大值为，则的图象向右平移后的表达式为___________．

已知函数f（x）=sinx+cosx．
（1）若f（x）=2f（﹣x），求的值；
（2）求函数F（x）=f（x）•f（﹣x）+f²（x）的最大值和单调递增区间．

关于函数f（x）=4sin（2x+），（x∈R）有下列命题：
①y=f（x）是以2π为最小正周期的周期函数；
②y=f（x）可改写为y=4cos（2x﹣）；
③y=f（x）的图象关于点（﹣，0）对称； 
④y=f（x）的图象关于直线x=对称；
其中正确的序号为      ．

已知函数．
（1）设，将函数表示为关于的函数，求的解析式；
（2）对任意，不等式恒成立，求的取值范围．

设函数，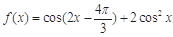
（Ⅰ）求的最大值，并写出使取最大值时x的集合；
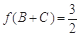（Ⅱ）已知中，角A、B、C的对边分别为a、b、c，若，，求的面积的最大值．

（本小题满分12分）已知函数（）在时有最小值．
（Ⅰ）求的值；
（Ⅱ）在中，，，分别是角，，所对的边，已知，，，求角的值．