设函数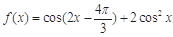 ,
,
(Ⅰ)求 的最大值,并写出使
的最大值,并写出使 取最大值时x的集合;
取最大值时x的集合;
(Ⅱ)已知 中,角A、B、C的对边分别为a、b、c,若
中,角A、B、C的对边分别为a、b、c,若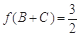 ,
, ,求
,求 的面积的最大值.
的面积的最大值.
某同学用“五点法”画函数 在某一个周期的图象时,列表并填入了部分数据,如下表:
在某一个周期的图象时,列表并填入了部分数据,如下表:
(1)请求出上表中的 ,
, ,
, ,并直接写出函数f(x)的解析式;
,并直接写出函数f(x)的解析式;
(2)将f(x)的图象沿x轴向右平移 个单位得到函数g(x),若函数g(x)在
个单位得到函数g(x),若函数g(x)在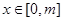 (其中
(其中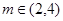 )上的值域为
)上的值域为 ,且此时其图象的最高点和最低点分别为P,Q,求
,且此时其图象的最高点和最低点分别为P,Q,求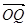 与
与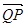 夹角
夹角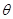 的大小.
的大小.
已知函数f(x)=2sinωxcosωx﹣2 sin2ωx+
sin2ωx+ (ω>0),直线x=x1,x=x2是函数y=f(x)的图象的任意两条对称轴,且|x1﹣x2|的最小值为
(ω>0),直线x=x1,x=x2是函数y=f(x)的图象的任意两条对称轴,且|x1﹣x2|的最小值为 .
.
(Ⅰ)求ω的值;
(Ⅱ)求函数f(x)的单调增区间;
(Ⅲ)若f(α)= ,求sin(
,求sin( π﹣4α)的值.
π﹣4α)的值.
已知向量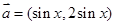 ,
,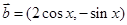 ,函数
,函数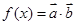 .
.
(1)求函数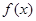 的最小正周期;
的最小正周期;
(2)求函数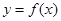 在
在 上的值域.
上的值域.
已知函数f(x)=sinx+cosx.
(1)若f(x)=2f(﹣x),求 的值;
的值;
(2)求函数F(x)=f(x)•f(﹣x)+f2(x)的最大值和单调递增区间.
已知函数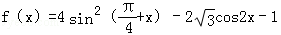 ,且给定条件p:“
,且给定条件p:“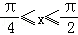 ”,
”,
(1)求f(x)的最大值及最小值
(2)若又给条件q:“|f(x)﹣m|<2“且p是q的充分条件,求实数m的取值范围.