高中数学简单的等周问题解答题

设命题：实数满足，其中；命题：实数满足且的必要不充分条件，求实数的取值范围．

已知命题p：方程2x²＋ax－a²＝0在[－1,1]上有解；命题q：只有一个实数x₀满足不等式x₀²＋2ax₀＋2a≤0，若命题“p∨q”是假命题，求实数a的取值范围．

命题p：∀x∈(1，＋∞)，函数f(x)＝|log₂x|的值域为[0，＋∞)；命题q：∃m≥0，使得y＝sin mx的周期小于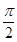，试判断p∨q，p∧q，p的真假性．

设命题p:函数的定义域为R;命题q:不等式,对∈(-∞,-1)上恒成立,如果命题“p∨q”为真命题,命题“p∧q”为假命题,求实数的取值范围.

设命题，若同时为假命题，求x的取值集合．

设命题函数的定义域为R，命题不等式对一切正实数x均成立，如果命题为真，为假，求实数a的取值范围.

已知，设p：函数在(0，＋∞)上单调递减，
q：曲线y＝x²＋(2a 3)x＋1与x轴交于不同的两点．若“p且q”为假，“﹁q”为假，求a的取值范围．

已知命题，命题。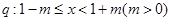
（1）若p是q的充分条件，求实数m的取值范围；
（2）若m=5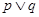，“ ”为真命题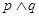，“ ”为假命题，求实数x的取值范围。

已知命题，命题。
（1）若p是q的充分条件，求实数m的取值范围；
（2）若m=5，“ ”为真命题，“ ”为假命题，求实数x的取值范围。

命题:“方程表示双曲线”()；命题:定义域为.若命题为真命题，为假命题，求实数的取值范围.

设命题p:函数的定义域为R;
命题q:不等式,对∈(-∞,-1)上恒成立,
如果命题“”为真命题,命题“”为假命题,求实数的取值范围.

设命题p:实数x满足,其中,命题实数满足.
(1)若且为真,求实数的取值范围;
(2)若是的充分不必要条件,求实数a的取值范围.

已知命题：方程有两个不相等的负实根，命题：恒成立；若或为真，且为假，求实数的取值范围．

已知命题：方程有两个不相等的负实根，命题：恒成立；若或为真，且为假，求实数的取值范围．

设命题命题，如果命题真且命题假，求的取值范围。