高考数学一轮配套特训:1-3简单的逻辑联结词全称量词与存在量词
下列命题中的假命题是( )
| A.∃x∈R,lnx=0 | B.∃x∈R,tanx=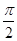 |
| C.∀x∈R,x2>0 | D.∀x∈R,3x>0 |
下列说法中正确的是( )
| A.“x>5”是“x>3”的必要不充分条件 |
| B.命题“对∀x∈R,恒有x2+1>0”的否定是“∃x∈R,使得x2+1≤0” |
| C.∃m∈R,使函数f(x)=x2+mx(x∈R)是奇函数 |
| D.设p,q是简单命题,若p∨q是真命题,则p∧q也是真命题 |
已知命题p:若(x-1)(x-2)≠0,则x≠1且x≠2;命题q:存在实数x0,使2x0<0.下列选项中为真命题的是( )
A.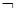 p p |
B.q | C.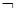 p∨q p∨q |
D.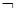 q∧p q∧p |
命题p:函数f(x)=x3-3x在区间(-1,1)内单调递减,命题q:函数f(x)=|sin2x|的最小正周期为π,则下列命题为真命题的是( )
| A.p∧q | B.( p)∨q p)∨q |
| C.p∨q | D.( p)∧( p)∧( q) q) |
已知“命题p:∃x∈R,使得ax2+2x+1<0成立”为真命题,则实数a满足( )
| A.[0,1) | B.(-∞,1) |
| C.[1,+∞) | D.(-∞,1] |
已知命题p:∃x∈R,x2+1<2x;命题q:若mx2-mx-1<0恒成立,则-4<m≤0,那么( )
A.“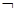 p”是假命题 p”是假命题 |
B.“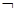 q”是真命题 q”是真命题 |
| C.“p∧q”为真命题 | D.“p∨q”为真命题 |
已知命题p:∃x∈R,使tanx=1,命题q:x2-3x+2<0的解集是{x|1<x<2}.下列结论:①命题“p∧q”是真命题; ②命题“p∧( q)”是假命题;③命题“(
q)”是假命题;③命题“( p)∨q”是真命题;④命题“(
p)∨q”是真命题;④命题“( p)∨(
p)∨( q)”是假命题.其中正确的是________.(填所有正确命题的序号)
q)”是假命题.其中正确的是________.(填所有正确命题的序号)
已知命题p:m∈R,且m+1≤0,命题q:∀x∈R,x2+mx+1>0恒成立,若p∧q为假命题,则m的取值范围是________.
下列说法正确的是________(将所有正确的序号填在横线上).
①直线l1:ax+y=3,l2:x+by-c=0,则l1∥l2的必要条件是ab=1;
②方程x2+mx+1=0有两个负根的充要条件是m>0;
③命题“若|a|=|b|,则a=b”为真命题;
④“x<0”是“x2-3x+2>0”的充分不必要条件.
设命题p:函数f(x)=lg(ax2-4x+a)的定义域为R;命题q:不等式2x2+x>2+ax,在x∈(-∞,-1)上恒成立,如果命题“p∨q”为真命题,命题“p∧q”为假命题,求实数a的取值范围.
已知命题P:函数y=loga(1-2x)在定义域上单调递增;命题Q:不等式(a-2)x2+2(a-2)x-4<0对任意实数x恒成立.若P∨Q是真命题,求实数a的取值范围.
已知命题p:函数f(x)=x2+ax-2在[-1,1]内有且仅有一个零点.命题q:x2+3(a+1)x+2≤0在区间[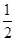 ,
, ]内恒成立.若命题“p且q”是假命题,求实数a的取值范围.
]内恒成立.若命题“p且q”是假命题,求实数a的取值范围.
已知命题p:∀x∈(1,+∞),log2x<log3x;命题q:∃x∈(0,+∞),2-x=lnx.则下列命题中为真命题的是( )
| A.p∧q | B.( p)∧q p)∧q |
C.p∧( q) q) |
D.( p)∧( p)∧( q) q) |
给出下面四个命题:
p1:∃x∈(0,+∞),( )x<(
)x<( )x;
)x;
p2:∃x∈(0,1), x>
x> x;
x;
p3:∀x∈(0,+∞),( )x>
)x> x;
x;
p4:∀x∈(0, ),(
),( )x<
)x< x.
x.
其中的真命题是( )
| A.p1,p3 | B.p1,p4 | C.p2,p3 | D.p2,p4 |
若函数f(x)=x2-2x,g(x)=ax+2(a>0),∀x1∈[-1,2],∃x0∈[-1,2],使g(x1)=f(x0),则a的取值范围是( )
A.(0, ] ] |
B.[ ,3] ,3] |
C.[3,+∞) | D.(0,3] |
 粤公网安备 44130202000953号
粤公网安备 44130202000953号