给出下列五个命题中,其中所有正确命题的序号是_______.
①函数 的最小值是3
的最小值是3
②函数 若
若 且
且 ,则动点
,则动点 到直线
到直线 的
的
最小距离是 .
.
③命题“函数 当
当
 ”是真命题.
”是真命题.
④函数 的最小正周期是1的充要条件是
的最小正周期是1的充要条件是 .
.
⑤已知等差数列 的前
的前 项和为
项和为 ,
, 为不共线的向量,又
为不共线的向量,又
若 ,则
,则 .
.
定义在R上的函数 ,若对任意
,若对任意 ,都有
,都有 ,则称f(x)为“H函数”,给出下列函数:
,则称f(x)为“H函数”,给出下列函数:
① ;
;
② ;
;
③ ;
;
④
其中是“H函数”的个数为( )
| A.4 | B.3 | C.2 | D.1 |
对于三次函数 ,给出定义:设
,给出定义:设 是函数y=f(x)的导数,
是函数y=f(x)的导数, 是
是 的导数,若方程
的导数,若方程 有实数解
有实数解 ,则称点
,则称点 为函数y=f(x)的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.
为函数y=f(x)的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.
设函数 ,则
,则 =( )
=( )
| A.2014 | B.2013 | C. |
D.1007 |
对于函数 和
和 ,设
,设 ,
, ,若存在
,若存在 ,使得
,使得 ,则称
,则称 与
与 互为“零点相邻函数”.若函数
互为“零点相邻函数”.若函数 与
与 互为“零点相邻函数”,则实数
互为“零点相邻函数”,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
若函数f(x)为定义域D上的单调函数,且存在区间 (其中a<b),使得当x∈[a,b]时,f(x)的取值范围恰为[a,b],则称函数f(x)是D上的“正函数”,若
(其中a<b),使得当x∈[a,b]时,f(x)的取值范围恰为[a,b],则称函数f(x)是D上的“正函数”,若 是
是 上的正函数,则实数k的取值范围是
上的正函数,则实数k的取值范围是
(小题满分14分)已知定义域为R的函数 是奇函数.
是奇函数.
(1)求 的值;
的值;
(2)若对任意的 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
若直角坐标平面内的两个不同点 、
、 满足条件:①
满足条件:① 、
、 都在函数
都在函数 的图像上;②
的图像上;② 、
、 关于原点对称,则称点对
关于原点对称,则称点对 是函数
是函数 的一对“友好点对”(注:点对
的一对“友好点对”(注:点对 与
与 看作同一对“友好点对”).已知函数
看作同一对“友好点对”).已知函数 =
= ,则此函数的“友好点对”有 ( )对.
,则此函数的“友好点对”有 ( )对.
| A.0 | B.1 | C.2 | D.3 |
(本小题满分14分)若在定义域内存在实数 ,使得
,使得 成立,则称函数有“飘移点”
成立,则称函数有“飘移点” .
.
(1)函数 是否有“飘移点”?请说明理由;
是否有“飘移点”?请说明理由;
(2)证明函数 在
在 上有“飘移点”;
上有“飘移点”;
(3)若函数 在
在 上有“飘移点”,求实数
上有“飘移点”,求实数 的取值范围.
的取值范围.
如果对定义在R上的函数 ,对任意
,对任意 ,都有
,都有 则称函数
则称函数 为“H函数”.给出下列函数:
为“H函数”.给出下列函数:
① ;
;
② ;
;
③ ;
;
④ .
.
其中函数式“H函数”的个数是( )
| A.4 | B.3 | C.2 | D.1 |
对于三次函数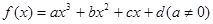 ,给出定义:设
,给出定义:设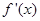 是函数
是函数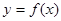 的导数,
的导数,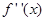 是
是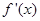 的导数,若方程
的导数,若方程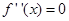 有实数解
有实数解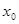 ,则称点
,则称点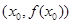 为函数
为函数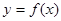 的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”,任何一个三次函数都有对称中心,且“拐点”就是对称中心。设函数
的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”,任何一个三次函数都有对称中心,且“拐点”就是对称中心。设函数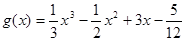 ,则
,则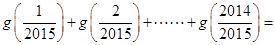 ( )
( )
| A.1 | B.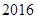 |
C.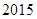 |
D.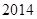 |
已知函数 的定义域为
的定义域为 ,若
,若 在
在 上为增函数,则称
上为增函数,则称
 为“比增函数”;
为“比增函数”;
(Ⅰ)若函数 是“比增函数”,求实数
是“比增函数”,求实数 的取值范围;
的取值范围;
(Ⅱ)已知 ,
, 为“比增函数”,且
为“比增函数”,且 的部分函数值由下表给出,
的部分函数值由下表给出,
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
求证: .
.