高中数学函数迭代试题

(本题满分18分)本题共有3个小题，第1小题满分6分，第2小题满分6分，第3小题满分6分．
已知函数．
(1) 试说明函数的图像是由函数的图像经过怎样的变换得到的；
(2) (理科)若函数，试判断函数的奇偶性，并用反证法证明函数的最小正周期是；
(3) 求函数的单调区间和值域．

（本小题满分12分）设函数在上的导函数为，在上的导函数为，若在上，恒成立，则称函数在上为“凸函数”．已知．
（1）若为区间上的“凸函数”，试确定实数的值；
（2）若当实数满足时，函数在上总为“凸函数”，求的最大值．

定义在上的函数,如果对于任意给定的等比数列，仍是等比数列,则称为“等比函数”.现有定义在上的如下函数:①；②； ③； ④.则其中是“等比函数”的的序号为      ．

若直角坐标平面内两点满足条件：①点都在的图象上；②点关于原点对称，则对称点对是函数的一个“兄弟点对”（点对与可看作一个“兄弟点对”）．已知函数, 则的“兄弟点对”的个数为

A．2

B．3

C．4

D．5

如果对于函数的定义域内任意两个自变量的值，当时，都有且存在两个不相等的自变量，使得，则称为定义域上的不严格的增函数．已知函数的定义域、值域分别为，，，且为定义域上的不严格的增函数，那么这样的函数共有________个．

德国著名数学家狄利克雷在数学领域成就显著，以其名命名的函数被称为狄利克雷函数，其中为实数集，为有理数集，则关于函数有如下四个结论：
①；
②函数是偶函数；
③任取一个不为零的有理数，对任意的恒成立；
④存在三个点，，，使得为等边三角形．
其中正确结论的个数是（  ）

A．

B．

C．

D．

（本小题满分14分）对于定义域为的函数，若同时满足下列条件：①在内单调递增或单调递减；②存在区间，使在上的值域为；那么把（）叫闭函数，且条件②中的区间为的一个“好区间”．
（1）求闭函数的“好区间”；
（2）若为闭函数的“好区间”，求、的值；
（3）判断函数是否为闭函数？若是闭函数，求实数的取值范围．

设m是一个非负整数，m的个位数记作，如，，，称这样的函数为尾数函数．给出下列有关尾数函数的结论：
①；
②，若，都有；]
③；
则正确的结论的个数为（  ）

A．3

B．2

C．1

D．0

在集合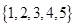中，任取一个偶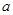数和一个奇数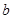，构成以原点为起点的向量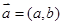．从所有得到的以原点为起点的向量中，任取两个向量为邻边作平行四边形，记所有作成的平行四边形的个数为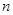，其中面积等于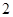的平行四边形的个数为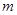，则（ ）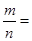

A．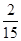

B．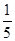

C．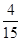

D．

定义在上的函数，如果对于任意给定的等比数列，仍是等比数列，则称为“保等比数列函数”． 现有定义在上的如下函数：
①     ②      ③    ④．
则其中是“保等比数列函数”的的序号为

A．①②

B．③④

C．①③

D．②④

设m是一个非负整数，m的个位数记作，如，，，称这样的函数为尾数函数．给出下列有关尾数函数的结论：
①；
②，若，都有；
③；
④．
则正确的结论的个数为（    ）

A．1

B．2

C．3

D．4

函数，其中，若动直线与函数的图像有三个不同的交点，它们的横坐标分别为，则是否存在最大值？若存在，在横线处填写其最大值；若不存在，直接填写“不存在”______________．

(本小题满分16分)对于函数，如果存在实数使得，那么称为的生成函数．
（1）下面给出两组函数，是否分别为的生成函数？并说明理由；
第一组：；
第二组：；
（2）设，生成函数．若不等式在上有解，求实数的取值范围.

定义函数，若存在常数，对于任意，存在唯一的，使得，则称函数在上的“均值”为，已知，则函数在上的“均值”为______．

对函数，在使成立的所有常数中，我们把的最大值叫做函数的下确界．现已知定义在R上的偶函数满足，当时，，则的下确界为 （    ）

A．

B．

C．

D．