定义:如果函数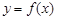 在定义域内给定区间
在定义域内给定区间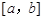 上存在
上存在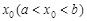 ,满足
,满足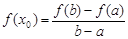 ,则称函数
,则称函数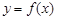 是
是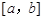 上的“平均值函数”,
上的“平均值函数”,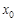 是它的一个均值点.例如
是它的一个均值点.例如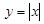 是
是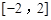 上的平均值函数,0就是它的均值点.若函数
上的平均值函数,0就是它的均值点.若函数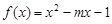 是
是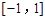 上的“平均值函数”,则实数m的取值范围是_________.
上的“平均值函数”,则实数m的取值范围是_________.
若函数 满足:在定义域D内存在实数
满足:在定义域D内存在实数 ,使得
,使得 成立,则称函数
成立,则称函数 为“1的饱和函数”.给出下列四个函数:①
为“1的饱和函数”.给出下列四个函数:① ;②
;② ;③
;③ ;④
;④ .其中是“1的饱和函数”的所有函数的序号为( ).
.其中是“1的饱和函数”的所有函数的序号为( ).
| A.①③ | B.②④ | C.①② | D.③④ |
定义:如果函数 在定义域内给定区间
在定义域内给定区间 上存在
上存在
 ,满足
,满足 ,则称函数
,则称函数 是
是 上的“平均值函数”,
上的“平均值函数”, 是它的一个均值点,例如
是它的一个均值点,例如 是
是 上的平均值函数,
上的平均值函数, 就是它的均值点.现有函数
就是它的均值点.现有函数 是
是 上的平均值函数,则实数
上的平均值函数,则实数 的取值范围是 .
的取值范围是 .
某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表.那么,各班可推选代表人数 与该班人数
与该班人数 之间的函数关系用取整函数
之间的函数关系用取整函数 (
( 表示不大于
表示不大于 的最大整数)可以表示为( )
的最大整数)可以表示为( )
A. |
B. |
C. |
D. |
某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表.那么,各班可推选代表人数 与该班人数
与该班人数 之间的函数关系用取整函数
之间的函数关系用取整函数 (
( 表示不大于
表示不大于 的最大整数)可以表示为 ( )
的最大整数)可以表示为 ( )
A. |
B. |
C. |
D. |
对于定义域和值域均为[0,1]的函数f(x),定义 ,
, ,…,
,…, ,n=1,2,3,….满足
,n=1,2,3,….满足 的点x∈[0,1]称为f的
的点x∈[0,1]称为f的 阶周期点.设
阶周期点.设 则f的
则f的 阶周期点的个数是
阶周期点的个数是
| A.2n | B.2(2n-1) | C.2n | D.2n2 |
(本小题满分14分)已知函数 ,
, ,设曲线
,设曲线 在点
在点 处的切线方程为
处的切线方程为 . 如果对任意的
. 如果对任意的 ,均有:
,均有:
①当 时,
时, ;
;
②当 时,
时, ;
;
③当 时,
时, ,
,
则称 为函数
为函数 的一个“ʃ-点”.
的一个“ʃ-点”.
(1)判断 是否是下列函数的“ʃ-点”:
是否是下列函数的“ʃ-点”:
① ; ②
; ② .(只需写出结论)
.(只需写出结论)
(2)设函数 .
.
(ⅰ)若 ,证明:
,证明: 是函数
是函数 的一个“ʃ-点”;
的一个“ʃ-点”;
(ⅱ)若函数 存在“ʃ-点”,直接写出
存在“ʃ-点”,直接写出 的取值范围.
的取值范围.
设函数 在
在 上有意义,对给定正数
上有意义,对给定正数 ,定义函数
,定义函数 则称函数
则称函数 为
为 的“孪生函数”,若给定函数
的“孪生函数”,若给定函数 ,则
,则 的值域为( )
的值域为( )
| A.[1,2] | B.[-1,2] | C. |
D. |
定义区间 ,
, ,
, ,
, 的长度均为
的长度均为 ,多个区间并集的长度为各区间长度之和,例如,
,多个区间并集的长度为各区间长度之和,例如,  的长度
的长度 .用
.用 表示不超过
表示不超过 的最大整数,记
的最大整数,记 ,其中
,其中 .设
.设 ,
, ,若用
,若用 分别表示不等式
分别表示不等式 ,方程
,方程 ,不等式
,不等式 解集区间的长度,则当
解集区间的长度,则当 时,有 ( )
时,有 ( )
A. |
B. |
C. |
D. |
如图,正方形 的顶点
的顶点 、
、 在反比例函数
在反比例函数 的图象上,顶点
的图象上,顶点 、
、 分别在
分别在 轴、
轴、 轴的正半轴上,再在其右侧作正方形
轴的正半轴上,再在其右侧作正方形 ,顶点
,顶点 、
、 在反比例函数
在反比例函数 的图象上,顶点
的图象上,顶点 在
在 轴的正半轴上,则点
轴的正半轴上,则点 的坐标为 .
的坐标为 .
我们称满足下面条件的函数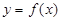 为“
为“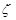 函数”:存在一条与函数
函数”:存在一条与函数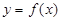 的图象有两个不同交点(设为
的图象有两个不同交点(设为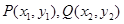 )的直线,
)的直线, 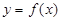 在
在 处的切线与此直线平行.下列函数:
处的切线与此直线平行.下列函数:
①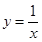 ②
②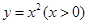 ③
③ ④
④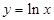 ,
,
其中为“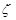 函数”的是 (将所有你认为正确的序号填在横线上)
函数”的是 (将所有你认为正确的序号填在横线上)