市内电话费是这样规定的,每打一次电话不超过3分钟付电话费0.18元,超过3分钟而不超过6分钟的付电话费0.36元,依次类推,每次打电话
 分钟应付话费y元,写出函数解析式并画出函数图象.
分钟应付话费y元,写出函数解析式并画出函数图象.
设f(x)=log (
( )为奇函数,a为常数.
)为奇函数,a为常数.
(Ⅰ)求a的值;
(Ⅱ)证明f(x)在(1,+∞)内单调递增;
(Ⅲ)若对于[3,4]上的每一个 的值,不等式
的值,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知函数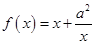 ,
,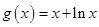 ,其中
,其中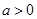 .
.
(1)若 是函数
是函数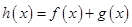 的极值点,求实数
的极值点,求实数 的值;
的值;
(2)若对任意的 (
(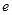 为自然对数的底数)都有
为自然对数的底数)都有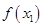 ≥
≥ 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知函数 ,
, ,函数
,函数 的图像在点
的图像在点 处的切线平行于
处的切线平行于 轴.
轴.
(1)求 的值;
的值;
(2)求函数 的极小值;
的极小值;
(3)设斜率为 的直线与函数
的直线与函数 的图象交于两点
的图象交于两点 ,(
,( )
)
证明: .
.
已知函数 ,
, (其中
(其中 ).
).
(Ⅰ)求函数 的极值;
的极值;
(Ⅱ)若函数 在区间
在区间 内有两个零点,求正实数a的取值范围;(Ⅲ)求证:当
内有两个零点,求正实数a的取值范围;(Ⅲ)求证:当 时,
时, .(说明:e是自然对数的底数,e=2.71828…)
.(说明:e是自然对数的底数,e=2.71828…)
已知函数 .
.
(1)求函数 的最大值;
的最大值;
(2)若函数 与
与 有相同极值点,
有相同极值点,
①求实数 的值;
的值;
②若对于 (
( 为自然对数的底数),不等式
为自然对数的底数),不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知函数f(x)=x2+2ax+3,x∈[-4,6].
(1)当a=-2时,求f(x)的最值;
(2)求实数a的取值范围,使y=f(x)在区间[-4,6]上是单调函数;
(3)当a=1时,求f(|x|)的单调区间.
已知函数 =
= ,其中a≠0.
,其中a≠0.
(1)若对一切x∈R, ≥1恒成立,求a的取值集合.
≥1恒成立,求a的取值集合.
(2)在函数 的图像上取定两点
的图像上取定两点 ,
,
 ,记直线AB的斜率为K,问:是否存在x0∈(x1,x2),使
,记直线AB的斜率为K,问:是否存在x0∈(x1,x2),使 成立?若存在,求
成立?若存在,求 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
已知函数 满足
满足 ,其中a>0,a≠1.
,其中a>0,a≠1.
(1)对于函数 ,当x∈(-1,1)时,f(1-m)+f(1-m2)<0,求实数m的取值集合;
,当x∈(-1,1)时,f(1-m)+f(1-m2)<0,求实数m的取值集合;
(2)当x∈(-∞,2)时,
 的值为负数,求
的值为负数,求 的取值范围。
的取值范围。
(1)已知函数y=ln(-x2+x-a)的定义域为(-2,3),求实数a的取值范围;
(2)已知函数y=ln(-x2+x-a)在(-2,3)上有意义,求实数a的取值范围.
已知函数 .
.
(I)当a=3时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(II)对任意b>0,f(x)在区间[b-lnb,+∞)上是增函数,求实数a的取值范围.