已知函数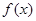
=
，其中a≠0．
（1）若对一切x∈R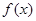，≥1恒成立，求a的取值集合．
（2）在函数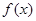的图像上取定两点
，
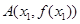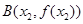
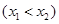，记直线AB的斜率为K，问：是否存在x0∈（x1，x2），使
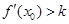成立？若存在，求
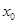的取值范围；若不存在，请说明理由．
相关知识点
推荐套卷
已知函数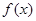=，其中a≠0．
（1）若对一切x∈R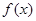，≥1恒成立，求a的取值集合．
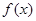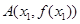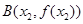
（2）在函数的图像上取定两点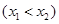，，记直线AB的斜率为K，问：是否存在x0∈（x1，x2），使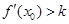成立？若存在，求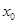的取值范围；若不存在，请说明理由．
粤公网安备 44130202000953号