(本题12分)某鲜花店每天以每束2.5元购入新鲜玫瑰花并以每束5元的价格销售,店主根据以往的销售统计得到每天能以此价格售出的玫瑰花数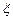 的分布列如表所示。若某天所购进的玫瑰花未售完,则当天未售出的玫瑰花将以每束1.5元的价格降价处理完毕。
的分布列如表所示。若某天所购进的玫瑰花未售完,则当天未售出的玫瑰花将以每束1.5元的价格降价处理完毕。
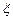 |
30 |
40 |
50 |
| P |
 |
 |
 |
(1)若某天店主购入玫瑰花40束,试求该天从玫瑰花销售中所获利润的期望;
(2)店主每天玫瑰花的进货量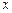
 ,单位:束
,单位:束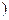 为多少时,其有望从玫瑰花销售中获得最大利润?
为多少时,其有望从玫瑰花销售中获得最大利润?
相关知识点
推荐套卷
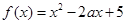 (
(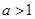 ).
).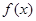 的定义域和值域均是
的定义域和值域均是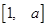 ,求实数
,求实数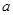 的值;
的值;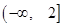 上是减函数,且对任意的
上是减函数,且对任意的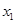 ,
,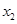
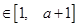 ,总有
,总有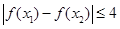 ,求实数
,求实数 :函数
:函数 在
在 内单调递减;
内单调递减; :曲线
:曲线 与
与 轴交于不同的两点.
轴交于不同的两点. 的取值范围;
的取值范围;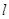 (宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数
(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数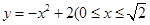 )的图象,且点M到边OA距离为
)的图象,且点M到边OA距离为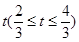 .
.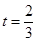 时,求直路
时,求直路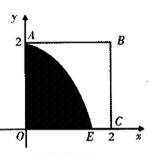
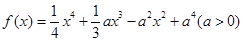
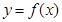 的单调区间;
的单调区间;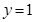 恰有两个交点,求
恰有两个交点,求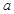 的取值范围.
的取值范围.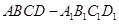 中,P是侧棱
中,P是侧棱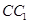 上的一点,
上的一点,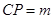 .
.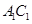 上是否存在一个定点
上是否存在一个定点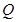 ,使得对任意的m,
,使得对任意的m,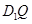 ⊥AP,并证明你的结论.
⊥AP,并证明你的结论.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号