(本题12分)根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
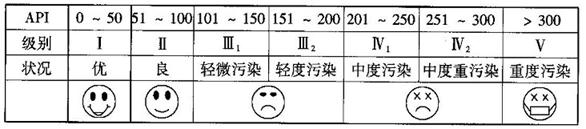
对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间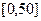 ,
,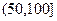 ,
,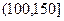 ,
, ,
,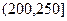 ,
,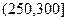 进行分组,得到频率分布直方图如图.
进行分组,得到频率分布直方图如图.
(1)求直方图中 的值;
的值;
(2)计算一年中空气质量为良的天数;
(3)某环保部门准备在一年内随机到该城市考察两次空气质量,求两次考察空气质量都为良的概率(结果用分数表示).
相关知识点
推荐套卷
(本题12分)根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:

对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间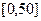 ,
,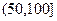 ,
,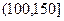 ,
, ,
,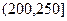 ,
,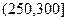 进行分组,得到频率分布直方图如图.
进行分组,得到频率分布直方图如图.
(1)求直方图中 的值;
的值;
(2)计算一年中空气质量为良的天数;
(3)某环保部门准备在一年内随机到该城市考察两次空气质量,求两次考察空气质量都为良的概率(结果用分数表示).