[辽宁]2012-2013学年辽宁朝阳柳城高中高二下学期期中考试理科数学试卷
用反证法证明某命题时,对其结论:“自然数 中恰有一个偶数”正确的反设为( )
中恰有一个偶数”正确的反设为( )
A. 都是奇数 都是奇数 |
B. 都是偶数 都是偶数 |
C. 中至少有两个偶数 中至少有两个偶数 |
D. 中至少有两个偶数或都是奇数 中至少有两个偶数或都是奇数 |
来源:2012-2013学年辽宁朝阳柳城高中高二下学期期中考试理科数学试题
有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线 平面
平面 ,直线
,直线 平面
平面 ,直线
,直线 ∥平面
∥平面 ,则直线
,则直线 ∥直线
∥直线 ”的结论显然是错误的,这是因为( )
”的结论显然是错误的,这是因为( )
| A.大前提错误 | B.小前提错误 |
| C.推理形式错误 | D.非以上错误 |
来源:2012-2013学年辽宁朝阳柳城高中高二下学期期中考试理科数学试题
函数f(x)=(x-3)ex的单调递增区间是( )
| A.(-∞,2) | B.(0,3) | C.(1,4) | D.(2,+∞) |
来源:2012-2013学年辽宁朝阳柳城高中高二下学期期中考试理科数学试题
给出定义:若函数 在D上可导,即
在D上可导,即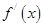 存在,且导函数
存在,且导函数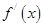 在D上也可导,则称
在D上也可导,则称 在D上存在二阶导函数,记
在D上存在二阶导函数,记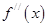 =
=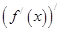 ,若
,若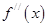 <0在D上恒成立,则称
<0在D上恒成立,则称 在D上为凸函数,以下四个函数在
在D上为凸函数,以下四个函数在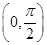 上不是凸函数的是( )
上不是凸函数的是( )
A. = = |
B. = =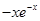 |
C. = =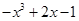 |
D. = =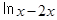 |
来源:2012-2013学年辽宁朝阳柳城高中高二下学期期中考试理科数学试题
若函数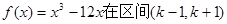 上不是单调函数,则实数k的取值范围是( )
上不是单调函数,则实数k的取值范围是( )
A. |
B.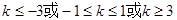 |
C. |
D.不存在这样的实数k |
来源:2012-2013学年辽宁朝阳柳城高中高二下学期期中考试理科数学试题
根据右边给出的数塔猜测123456 9+8=( )
9+8=( ) 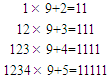
| A.1111110 |
| B.1111111 |
| C.1111112 |
| D.1111113 |
来源:2012-2013学年辽宁朝阳柳城高中高二下学期期中考试理科数学试题
设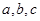 小于0,则3个数:
小于0,则3个数: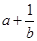 ,
, ,
,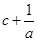 的值 ( )
的值 ( )
| A.至多有一个不小于-2 | B.至多有一个不大于2 |
| C.至少有一个不大于-2 | D.至少有一个不小于2 |
来源:2012-2013学年辽宁朝阳柳城高中高二下学期期中考试理科数学试题
已知函数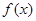 的定义域为
的定义域为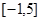 ,部分对应值如下表。
,部分对应值如下表。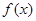 的导函数
的导函数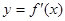 的图像如图所示。
的图像如图所示。
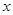 |
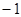 |
0 |
 |
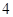 |
 |
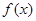 |
 |
 |
 |
 |
 |
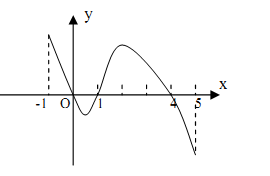
下列关于函数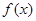 的命题:
的命题:
①函数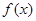 在
在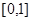 上是减函数;②如果当
上是减函数;②如果当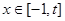 时,
时,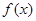 最大值是
最大值是 ,那么
,那么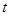 的最大值为
的最大值为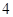 ;③函数
;③函数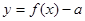 有
有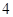 个零点,则
个零点,则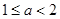 ;④已知
;④已知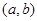 是
是 的一个单调递减区间,则
的一个单调递减区间,则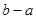 的最大值为
的最大值为 。
。
其中真命题的个数是( )
A、4个 B、3个 C、2个 D、1个
来源:2012-2013学年辽宁朝阳柳城高中高二下学期期中考试理科数学试题
在平面直角坐标系中,以坐标原点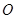 为几点,
为几点, 轴的正半轴为极轴建立极坐标系.已知直线
轴的正半轴为极轴建立极坐标系.已知直线 上两点
上两点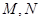 的极坐标分别为
的极坐标分别为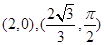 ,圆
,圆 的参数方程
的参数方程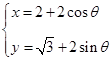 (
(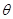 为参数).
为参数).
(Ⅰ)设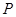 为线段
为线段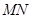 的中点,求直线
的中点,求直线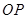 的平面直角坐标方程;
的平面直角坐标方程;
(Ⅱ)判断直线 与圆
与圆 的位置关系.
的位置关系.
来源:2012-2013学年辽宁朝阳柳城高中高二下学期期中考试理科数学试题
已知函数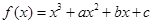 ,曲线
,曲线 在点
在点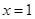 处的切线为
处的切线为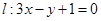 ,若
,若 时,
时, 有极值.
有极值.
(1)求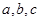 的值;
的值;
(2)求 在
在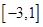 上的最大值和最小值.
上的最大值和最小值.
来源:2012-2013学年辽宁朝阳柳城高中高二下学期期中考试理科数学试题
 , 则
, 则 等于( )
等于( )



 ,则
,则 的值为( )
的值为( )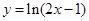 上的点到直线
上的点到直线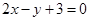 的最短距离是 ( )
的最短距离是 ( )

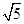
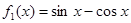 ,
,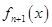 是
是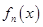 的导函数,即
的导函数,即 ,
,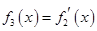 ,…,
,…, ,
, ,则
,则

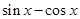
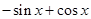
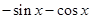
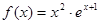 ,
, 的最大值为
的最大值为  是偶函数,若曲线
是偶函数,若曲线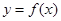 在点
在点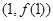 处的切线的斜率为1,则该曲线在点
处的切线的斜率为1,则该曲线在点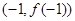 处的切线的斜率为
处的切线的斜率为  ,观察:
,观察: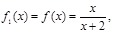
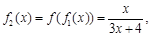

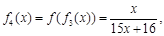
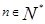 且
且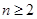 时,
时,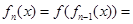 .
.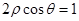 与圆
与圆 相交的弦长为___________.
相交的弦长为___________.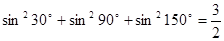
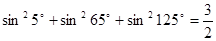
 ,那么
,那么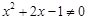 。
。 满足:
满足: 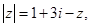 (1)求
(1)求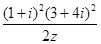 的共轭复数
的共轭复数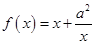 ,
,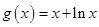 ,其中
,其中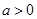 .
. 是函数
是函数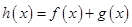 的极值点,求实数
的极值点,求实数 的值;
的值; (
(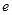 为自然对数的底数)都有
为自然对数的底数)都有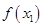 ≥
≥ 成立,求实数
成立,求实数 粤公网安备 44130202000953号
粤公网安备 44130202000953号