已知函数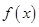
满足
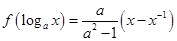，其中a>0,a≠1．
（1）对于函数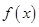，当x∈（-1,1）时，f（1-m）+f（1-m2）<0,求实数m的取值集合；
（2）当x∈（-∞,2）时，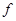
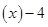的值为负数，求
的取值范围。
相关试题
个人坐在一排
个座位上,问(1)空位不相邻的坐法有多少种?
个空位只有
个相邻的坐法有多少种?
个相邻的坐法有多少种?
，被甲或乙解出的概率为
，（1）求该题被乙独立解出的概率；
的数学期望和方差
中，
，点
是
的中点.
；（2）
平面
.
是公差为正数的等差数列，若
,
。
，
，求
。相关知识点
推荐套卷
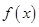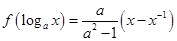已知函数满足，其中a>0,a≠1．
（1）对于函数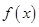，当x∈（-1,1）时，f（1-m）+f（1-m2）<0,求实数m的取值集合；
（2）当x∈（-∞,2）时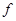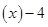，的值为负数，求的取值范围。
粤公网安备 44130202000953号