已知y=f(x)是定义在R上的奇函数,当x≤0时,f(x)=2x+x2.
(1)求x>0时,f(x)的解析式;
(2)若关于x的方程f(x)=2a2+a有三个不同的解,求a的取值范围.
若存在实常数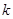 和
和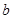 ,使得函数
,使得函数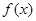 和
和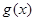 对其定义域上的任意实数
对其定义域上的任意实数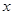 分别满足:
分别满足: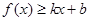 和
和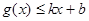 ,则称直线
,则称直线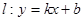 为
为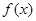 和
和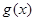 的“隔离直线”.已知
的“隔离直线”.已知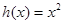 ,
,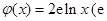 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求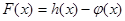 的极值;
的极值;
(Ⅱ)函数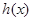 和
和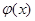 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
已知曲线 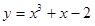 在点
在点 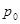 处的切线
处的切线 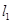 平行直线
平行直线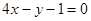 ,且点
,且点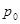 在第三象限.
在第三象限.
(Ⅰ)求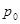 的坐标;
的坐标;
(Ⅱ)若直线 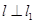 , 且
, 且  也过切点
也过切点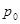 ,求直线
,求直线 的方程.
的方程.
已知 的图象过原点,且在点
的图象过原点,且在点 处的切线与
处的切线与 轴平行.对任意
轴平行.对任意 ,都有
,都有 .
.
(1)求函数 在点
在点 处切线的斜率;
处切线的斜率;
(2)求 的解析式;
的解析式;
(3)设 ,对任意
,对任意 ,都有
,都有 .求实数
.求实数 的取值范围
的取值范围
设 ,函数
,函数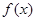 的图像与函数
的图像与函数 的图像关于点
的图像关于点 对称.
对称.
(1)求函数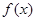 的解析式;
的解析式;
(2)若关于 的方程
的方程 有两个不同的正数解,求实数
有两个不同的正数解,求实数 的取值范围.
的取值范围.
已知函数 .
.
(1)当 时,求
时,求 的单调区间,如果函数
的单调区间,如果函数 仅有两个零点,求实数
仅有两个零点,求实数 的取值范围;
的取值范围;
(2)当 时,试比较
时,试比较 与1的大小.
与1的大小.