高中数学函数迭代解答题

已知函数，
（1）求的极值；
（2）若关于x的不等式在上恒成立，求k的取值范围；
（3）证明：.

已知函数，，且．
（Ⅰ）若，求的值；
（Ⅱ）当时，求函数的最大值；
（Ⅲ）求函数的单调递增区间．

已知函数.
（Ⅰ）当a=0时，求函数f(x)的图像在点A(1,f(1))处的切线方程；
（Ⅱ）若f(x)在R上单调，求a的取值范围；
（Ⅲ）当时，求函数f(x)的极小值。

（本小题满分14分）
设函数
（I）求函数在区间[0，1]上的最小值；
（II）当时，记曲线在点处的切线为与x轴交于点，求证：

（本小题共14分）
已知函数.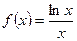
（I）判断函数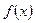的单调性；
（Ⅱ）若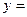+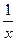的图像总在直线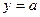的上方，求实数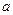的取值范围；
（Ⅲ）若函数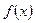与的图像有公共点，且在公共点处的切线相同，求实数的值.

已知函数的定义域为R，且当时，恒成立，
（1）求证：的图象关于点对称；
（2）求函数图象的一个对称点。

(本小题满分12分)
已知函数，其中，为实常数且
(Ⅰ)求的单调增区间；
(Ⅱ)若对任意恒成立，求实数的取值范围.

铁道机车运行1小时所需的成本由两部分组成，固定部分为元，变动部分与运行速度V（千米/小时）的平方成正比。比例系数为k（k≠0）。如果机车匀速从甲站开往乙站，为使成本最省应以怎样的速度运行？

已知水渠在过水断面面积为定值的情况下，过水湿周越小，其流量越大.现有以下两种设计，如图：

图①的过水断面为等腰△ABC，AB=BC，过水湿周
图②的过水断面为等腰梯形∥，过水湿周.若与梯形ABCD的面积都为S，
（I）分别求的最小值；
（II）为使流量最大，给出最佳设计方案.

已知，若求的范围。

对于任意，函数表示中的最大者，则的最小值是2．

某市空调公共汽车的票价按下列规则制定：
（1）5公里以内，票价2元；
（2）5公里以上，每增加5公里，票价增加1元（不足5公里的按5公里算）．
已知两个相邻的公共汽车站间相距约为1公里，如果沿途(包括起点和终点站)有21个汽车站，请根据题意，写出票价与里程之间的函数解析式，并画出函数的图象．

定义在上的函数是减函数，求满足不等式
的的集合．

中，，，、分别是、上的动点，且满足，若，，
（１）  写出的取值范围，
（２）  求的解析式．

一个圆柱形容器的底部直径是cm，高是cm．现在以cm／s的速度向容器内注入某种溶液．求容器内溶液的高度cm与注入溶液的时间s之间的函数解析式，并写出函数的定义域和值域．