高中数学不定方程和方程组解答题

已知关于x的二次方程
（1）若方程有两根，其中一根在区间内，另一根在区间内，求m的取值范围
（2）若方程两根均在区间内，求m的取值范围       

（本小题满分12分）
二次函数
（1）求的解析式；
（2）在区间上，的图象上方，求实数m的范围.

（本小题满分14分）已知函数f(x)满足对任意实数x，y都有f（x+y）=f（x）+f（y）+xy+1,且f（－2）=－2.
（1）求f（1）的值;
（2）证明:对一切大于1的正整数t，恒有f（t）>t;
（3）试求满足f（t）=t的整数的个数，并说明理由.

已知函数f(x)和g(x)的图象关于原点对称，且f(x)＝x²＋2x.
(1)求函数g(x)的解析式；
(2)解不等式g(x)≥f(x)－|x－1|；
(3)若h(x)＝g(x)－λf(x)＋1在[－1,1]上是增函数，求实数λ的取值范围

已知二次函数f(x)＝ax²＋bx＋c，(a<0)不等式f(x)>－2x的解集为(1,3)．
(1)若方程f(x)＋6a＝0有两个相等的实根，求f(x)的解析式；
(2)若f(x)的最大值为正数，求实数a的取值范围．

已知函数，当恒成立的a的最小值为k，存在n个
正数，且，任取n个自变量的值

（I）求k的值；
（II）如果
（III）如果，且存在n个自变量的值，使，求证：

（3）(本小题满分7分)选修4—5：不等式选讲
已知函数，不等式在上恒成立．
（Ⅰ）求的取值范围；
（Ⅱ）记的最大值为，若正实数满足，求的最大值．

设函数对任意都有且x>0时，<0, .(1)求在区间[-3，3]上的最大和最小值，（2）解关于x的不等式，（其中）

已知
（I）a=2时，求和的公共点个数；
（II）a为何值时，的公共点个数恰为两个。

已知函数，
（1）若函数的图象上有与轴平行的切线，求的取范围；
（2）若在时取得极值，且时，恒成立，求的取值范围。

某商场从生产厂家以每件元购进一批商品，若该商品零售价定为元，则销售量（单位：件）与零售价（单位：元）有如下关系：，问该商品零售价定为多少时利润最大，并求出最大利润（利润销售收入进货支出）

已知△ABC的周长为，且，
(1)求边AB的长；
(2)若△ABC的面积为，求角C的度数。

20．已知函数
（1）求函数的极值；
（2）设函数若函数在上恰有两个不同零点，求实数 的取值范围.

：已知函数，
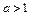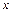（1）若，且关于的方程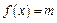有两个不同的正数解，求实数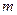的取值范围；
（2）设函数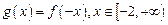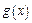，满足如下性质：若存在最大（小）值，则最大（小）值与无关.试求的取值范围．

已知函数
（1）求函数的对称轴方程；
（2）当时，若函数有零点，求m的范围；
（3）若，，求的值.