某商场从生产厂家以每件
元购进一批商品，若该商品零售价定为
元，则销售量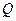
（单位：件）与零售价（单位：元）有如下关系：
，问该商品零售价定为多少时利润
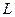最大，并求出最大利润（利润
销售收入
进货支出）
（
为参数，
）求证此抛物线顶点的轨迹是双曲线.
、
都是正数，
且
，求证：
.
均为正数，且
，求证
的线段两端点分别在直角坐标轴上移动，从原点向该线段作垂线，垂足为
，求
为⊙
的直径，
、
为⊙
、
为切点
，求AD·OC的值.相关知识点
推荐套卷
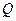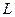某商场从生产厂家以每件元购进一批商品，若该商品零售价定为元，则销售量（单位：件）与零售价（单位：元）有如下关系：，问该商品零售价定为多少时利润最大，并求出最大利润（利润销售收入进货支出）
粤公网安备 44130202000953号