(本题16分)已知函数 ,其中e是自然数的底数,
,其中e是自然数的底数, ,
,
(1)当 时,解不等式
时,解不等式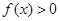 ;
;
(2)若当 时,不等式
时,不等式 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(3)当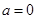 时,试判断:是否存在整数k,使得方程
时,试判断:是否存在整数k,使得方程 在
在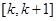
上有解?若存在,请写出所有可能的k的值;若不存在,说明理由。
已知定义在 上的函数
上的函数 =
=

(Ⅰ)若 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅱ)若 对
对 上的任意
上的任意 都成立,求实数
都成立,求实数 的取值范围;
的取值范围;
(Ⅲ)若 在[m,n]上的值域是[m,n](m≠n),求实数
在[m,n]上的值域是[m,n](m≠n),求实数 的取值范围
的取值范围
已知函数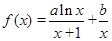 ,曲线
,曲线 在点
在点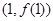 处的切线方程为
处的切线方程为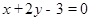 。
。
(Ⅰ)求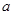 、
、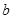 的值;
的值;
(Ⅱ)如果当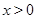 ,且
,且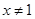 时,
时,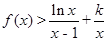 ,求
,求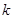 的取值范围
的取值范围
已知函数 ,
, ,k为非零实数.
,k为非零实数.
(Ⅰ)设t=k2,若函数f(x),g(x)在区间(0,+∞)上单调性相同,求k的取值范围;
(Ⅱ)是否存在正实数k,都能找到t∈[1,2],使得关于x的方程f(x)=g(x)在[1,5]上有且仅有一个实数根,且在[-5,-1]上至多有一个实数根.若存在,请求出所有k的值的集合;若不存在,请说明理由.
已知函数
(1)若函数 在
在 上为增函数,求正实数
上为增函数,求正实数 的取值范围;
的取值范围;
(2)当 时,求函数
时,求函数 在
在 上的最值;
上的最值;
(3)当 时,对大于1的任意正整数
时,对大于1的任意正整数 ,试比较
,试比较 与
与 的大小关系.
的大小关系.
已知函数 (
( 为常数).
为常数).
(1)若1为函数 的零点, 求
的零点, 求 的值;
的值;
(2)证明函数 在[0,2]上是单调递增函数;
在[0,2]上是单调递增函数;
(3)已知函数 , 求函数
, 求函数 的零点.
的零点.
函数 函数
函数 的图像如图所示。
的图像如图所示。
(Ⅰ)求 的值;
的值;
(Ⅱ)求函数 的单调区间。
的单调区间。
已知函数
(1)试求b,c所满足的关系式;
(2)若b=0,方程 有唯一解,求a的取值范围.
有唯一解,求a的取值范围.
已知函数y=f(x)对任意的实数ab都有:f(a+b)=f(a)+f(b)﹣1,且x>0时,f(x)>1,
(1)求证:f(x)是R上的增函数;
(2)若f(4)=5,求f(2)的值,并解不等式f(3m2﹣m﹣2)<3.