设函数 .
.
(Ⅰ)当 时,讨论函数
时,讨论函数 的零点个数;
的零点个数;
(Ⅱ)若对于给定的实数 ,存在实数
,存在实数 ,使不等式
,使不等式 对于任意
对于任意 恒成立。试将最大实数
恒成立。试将最大实数 表示为关于
表示为关于 的函数
的函数 ,并求
,并求 的取值范围.
的取值范围.
已知定义在R上的单调递增函数 满足
满足 ,且
,且 。
。
(Ⅰ)判断函数 的奇偶性并证明之;
的奇偶性并证明之;
(Ⅱ)解关于 的不等式:
的不等式: ;
;
(Ⅲ)设集合 ,
, .
. ,若集合
,若集合 有且仅有一个元素,求证:
有且仅有一个元素,求证:  。
。
已知函数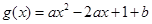 (
(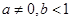 ),在区间
),在区间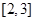 上有最大值4,最小值1,设
上有最大值4,最小值1,设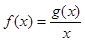 .
.
(1)求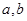 的值;
的值;
(2)不等式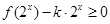 在
在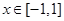 上恒成立,求实数
上恒成立,求实数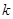 的取值范围;
的取值范围;
(3)方程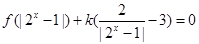 有三个不同的实数解,求实数
有三个不同的实数解,求实数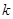 的取值范围.
的取值范围.
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为 立方米,且
立方米,且 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为 千元,设该容器的建造费用为
千元,设该容器的建造费用为 千元.
千元.
(Ⅰ)写出 关于
关于 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(Ⅱ)求该容器的建造费用最小时的 .
.
已知点 直线AM,BM相交于点M,且
直线AM,BM相交于点M,且 .
.
(1)求点M的轨迹 的方程;
的方程;
(2)过定点(0,1)作直线PQ与曲线C交于P,Q两点,且 ,求直线PQ的方程.
,求直线PQ的方程.
定义在(0,+∞)上的函数f(x),对于任意的m,n∈(0,+∞),都有f(mn)=f(m)+f(n)成立,当x>1时,f(x)<0.
(1)求证:1是函数f(x)的零点;
(2)求证:f(x)是(0,+∞)上的减函数;
(3)当f (2)=  时,解不等式f (ax+4)>1.
时,解不等式f (ax+4)>1.
已知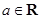 ,函数
,函数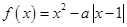 .
.
(Ⅰ)当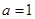 时,求函数
时,求函数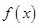 的最小值;
的最小值;
(Ⅱ)当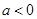 时,讨论
时,讨论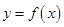 的图象与
的图象与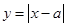 的图象的公共点个数.
的图象的公共点个数.
已知函数 是偶函数.
是偶函数.
(1)求k的值;
(2)若函数y=f(x)的图象与直线 没有交点,求b的取值范围.
没有交点,求b的取值范围.
(3)设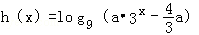 ,若函数f(x)与h(x)的图象有且只有一个公共点,求实数a的取值范围.
,若函数f(x)与h(x)的图象有且只有一个公共点,求实数a的取值范围.
已知函数 且
且 .
.
(Ⅰ) 若1是关于x的方程 的一个解,求t的值;
的一个解,求t的值;
(Ⅱ) 当 且
且 时,解不等式
时,解不等式 ;
;
(Ⅲ)若函数 在区间(-1,2]上有零点,求t的取值范围.
在区间(-1,2]上有零点,求t的取值范围.
已知函数 (
( 为自然对数的底数,
为自然对数的底数, ).
).
(1)判断曲线 在点
在点 处的切线与曲线
处的切线与曲线 的公共点个数;
的公共点个数;
(2)当 时,若函数
时,若函数 有两个零点,求a的取值范围.
有两个零点,求a的取值范围.
已知函数 .
.
(Ⅰ)当 时,证明:
时,证明: 为奇函数;
为奇函数;
(Ⅱ)若关于 的方程
的方程 有两个不等实数根,求实数
有两个不等实数根,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知函数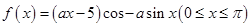 ,其中
,其中 为正实数。
为正实数。
(1)当 时,求
时,求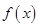 在
在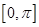 上的零点个数。
上的零点个数。
(2)对于定义域内的任意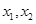 ,将
,将 的最大值记作
的最大值记作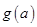 ,求
,求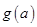 的表达式。
的表达式。