设已知函数 ,
,
(1)当 时,求函数
时,求函数 的最大值的表达式
的最大值的表达式
(2)是否存在实数 ,使得
,使得 有且仅有3个不等实根,且它们成等差数列,若存在,求出所有
有且仅有3个不等实根,且它们成等差数列,若存在,求出所有 的值,若不存在,说明理由.
的值,若不存在,说明理由.
(本小题满分12分)函数 (
( 为常数)的图象过点
为常数)的图象过点 .
.
(1)求 的值;
的值;
(2)函数 在区间
在区间 上有意义,求实数
上有意义,求实数 的取值范围;
的取值范围;
(3)讨论关于 的方程
的方程 (
( 为常数)的正根的个数.
为常数)的正根的个数.
设 为二次函数,且
为二次函数,且 ,
, .
.
(1)求 的解析式;
的解析式;
(2)设 ,若函数
,若函数 在实数
在实数 上没有零点,求
上没有零点,求 的取值范围.
的取值范围.
已知函数 是偶函数.
是偶函数.
(1)求k的值;
(2)若函数y=f(x)的图象与直线 没有交点,求b的取值范围.
没有交点,求b的取值范围.
(3)设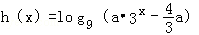 ,若函数f(x)与h(x)的图象有且只有一个公共点,求实数a的取值范围.
,若函数f(x)与h(x)的图象有且只有一个公共点,求实数a的取值范围.
已知函数 且
且 .
.
(Ⅰ) 若1是关于x的方程 的一个解,求t的值;
的一个解,求t的值;
(Ⅱ) 当 且
且 时,解不等式
时,解不等式 ;
;
(Ⅲ)若函数 在区间(-1,2]上有零点,求t的取值范围.
在区间(-1,2]上有零点,求t的取值范围.
已知函数 (
( 为自然对数的底数,
为自然对数的底数, ).
).
(1)判断曲线 在点
在点 处的切线与曲线
处的切线与曲线 的公共点个数;
的公共点个数;
(2)当 时,若函数
时,若函数 有两个零点,求a的取值范围.
有两个零点,求a的取值范围.
已知函数 .
.
(Ⅰ)当 时,证明:
时,证明: 为奇函数;
为奇函数;
(Ⅱ)若关于 的方程
的方程 有两个不等实数根,求实数
有两个不等实数根,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知函数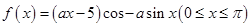 ,其中
,其中 为正实数。
为正实数。
(1)当 时,求
时,求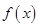 在
在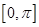 上的零点个数。
上的零点个数。
(2)对于定义域内的任意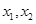 ,将
,将 的最大值记作
的最大值记作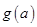 ,求
,求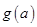 的表达式。
的表达式。