已知函数 的定义域为[2,3],值域为[1,4];设
的定义域为[2,3],值域为[1,4];设 .
.
(1)求a,b的值;
(2)若不等式 在
在 上恒成立,求实数k的取值范围;
上恒成立,求实数k的取值范围;
(3)若 有三个不同的实数解,求实数k的取值范围.
有三个不同的实数解,求实数k的取值范围.
已知函数 ,现将
,现将 的图像向右平移一个单位,再向上平移一个单位得到函数
的图像向右平移一个单位,再向上平移一个单位得到函数 的图像.
的图像.
(1)求函数 的解析式;
的解析式;
(2)函数 的图像与函数
的图像与函数 的图像在
的图像在 上至少有一个交点,求实数
上至少有一个交点,求实数 的取值范围.
的取值范围.
已知函数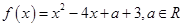
(1)若函数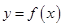 的图象与x轴无交点,求a的取值范围;
的图象与x轴无交点,求a的取值范围;
(2) 若函数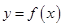 在[-1,1]上存在零点,求a的取值范围;
在[-1,1]上存在零点,求a的取值范围;
(3)设函数 ,当
,当 时,若对任意的
时,若对任意的 ,总存在
,总存在 ,使得
,使得 ,求b的取值范围.
,求b的取值范围.
已知函数f(x)= ,若存在实数a,b,c,d,满足f(a)=f(b)=f(c)=f(d),其中0<a<b<c<d,则abcd的取值范围 .
,若存在实数a,b,c,d,满足f(a)=f(b)=f(c)=f(d),其中0<a<b<c<d,则abcd的取值范围 .
函数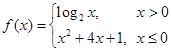 ,若实数
,若实数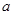 满足
满足 =1,则实数
=1,则实数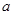 的所有取值的和为( )
的所有取值的和为( )
| A.1 | B. |
C. |
D.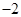 |