关于
的方程
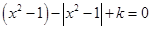，给出下列四个命题：
①存在实数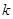
，使得方程恰有2个不同的实根
②存在实数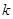，使得方程恰有4个不同的实根
③存在实数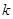，使得方程恰有5个不同的实根
④存在实数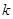，使得方程恰有8个不同的实根
其中假命题的个数是（ ）
| A．0 | B．1 | C．2 | D．3 |
相关试题
=（1，1，0），
=（﹣1，0，2）且k
=λ（
+
），则λ=（）
倾斜角是（）相关知识点
推荐套卷
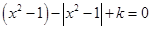关于的方程，给出下列四个命题：
①存在实数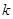，使得方程恰有2个不同的实根
②存在实数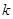，使得方程恰有4个不同的实根
③存在实数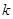，使得方程恰有5个不同的实根
④存在实数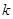，使得方程恰有8个不同的实根
其中假命题的个数是（ ）
| A．0 | B．1 | C．2 | D．3 |
粤公网安备 44130202000953号