(如图1)在平面四边形 中,
中, 为
为 中点,
中点, ,
, ,且
,且 ,现沿
,现沿 折起使
折起使 ,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.
,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.
(1)求三棱锥 的体积;
的体积;
(2)在线段PC上是否存在一点M,使直线 与直线
与直线 所成角为
所成角为 ?若存在,求出线段的长;若不存在,请说明理由.
?若存在,求出线段的长;若不存在,请说明理由.
(本小题满分12分)如图,四棱锥 中,底面四边形
中,底面四边形 为直角梯形,对角线
为直角梯形,对角线 交与点
交与点 ,
, ,
, 底面
底面 ,点
,点 为棱
为棱 上一动点。
上一动点。
(Ⅰ)证明: ;
;
(Ⅱ)若 平面
平面 ,求三棱锥
,求三棱锥 的体积.
的体积.
如图,已知直角梯形 所在的平面垂直于平面
所在的平面垂直于平面 ,
, ,
, ,
, .
.
(Ⅰ)点 是直线
是直线 中点,证明
中点,证明 平面
平面 ;
;
(Ⅱ)求平面 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(本小题满分12分)如下图,在组合体中, 是一个长方体,
是一个长方体, 是一个四棱锥.
是一个四棱锥. ,
, ,点
,点 且
且 .
.
(1)证明: ;
;
(2)求 与平面
与平面 所成的角的正切值;
所成的角的正切值;
(3)若 ,当
,当 为何值时,
为何值时, .
.
如图,在四棱锥A-BCDE中,侧面∆ADE是等边三角形,底面BCDE是等腰梯形,且CD∥BE,DE=2,CD=4, ,M是DE的中点,F是AC的中点,且AC=4,
,M是DE的中点,F是AC的中点,且AC=4,
求证:(1)平面ADE⊥平面BCD;
(2)FB∥平面ADE.
如图,三棱锥 中,
中, ,
,

(Ⅰ)求证: ;
;
(Ⅱ)若 ,
, 是
是 的中点,求
的中点,求 与平面
与平面 所成角的正切值
所成角的正切值
如图,在等腰梯形 中,
中, 是梯形的高,
是梯形的高, ,
, ,现将梯形沿
,现将梯形沿 折起,使
折起,使 ,且
,且 ,得一简单组合体
,得一简单组合体 如图所示,已知
如图所示,已知 分别为
分别为 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证: 平面
平面 .
.
已知在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, ,
, ,
, 分别是
分别是 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求二面角 的余弦值.
的余弦值.
如图,四棱锥 的底面是直角梯形,
的底面是直角梯形, ,
, ,
, 和
和 是两个边长为
是两个边长为 的正三角形,
的正三角形, ,
, 为
为 的中点,
的中点, 为
为 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题满分14分)在直三棱柱 中,
中,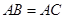 ,
, ,点
,点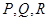 分别是棱
分别是棱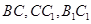 的中点.
的中点.
(1)求证: //平面
//平面 ;
;
(2)求证:平面
 平面
平面 .
.
(本小题满分14分)如图,在四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, 为
为 的中点,
的中点, 底面
底面 .
.
(1)求证: 平面
平面 ;
;
(2)在线段 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ?若存在,写出证明过程;若不存在,请说明理由.
?若存在,写出证明过程;若不存在,请说明理由.