高中数学平行线法解答题

（本小题满分14分）如图，在五面体ABC—DEF中，四边形BCFE 是矩形，DE 平面BCFE．

求证：（1）BC 平面ABED；
（2）CF // AD．

已知三棱柱中，侧棱垂直于底面，，，，，点在上．

（1）若是中点，求证：平面；
（2）当时，求二面角的余弦值．

（本小题12分）如图，已知直角梯形中，且，又分别为的中点，将△沿折叠，使得.

（Ⅰ）求证：AE⊥平面CDE；
（Ⅱ）求证：FG∥平面BCD；
（Ⅲ）在线段AE上找一点R，使得平面BDR⊥平面DCB， 并说明理由．

如图，在四棱锥S﹣ABCD中，底面ABCD是正方形，其他四个侧面都是等边三角形，AC与BD的交点为O，E为侧棱SC上一点．

（Ⅰ）当E为侧棱SC的中点时，求证：SA∥平面BDE；
（Ⅱ）求证：平面BDE⊥平面SAC；
（Ⅲ）（理科）当二面角E﹣BD﹣C的大小为45°时，试判断点E在SC上的位置，并说明理由．

（本小题满分12分）如图，四边形是正方形，平面，，，、、分别为、、的中点．
（1）求证：平面；
（2）求平面与平面所成锐二面角的大小.

（本小题满分14分）在四棱锥中,平面,是边长为4的正三角形,与的交点恰好是中点,又,点在线段上,且.

（1）求证：；
（2）求证：平面.

（本小题满分14分）如图，中，，四边形是矩形，，平面平面，、分别是、的中点，与平面所成角的正弦值为.

（Ⅰ）求证：∥底面；
（Ⅱ）求与面的所成角．

如图，△是等边三角形， ，，，，分别是，，的中点，将△沿折叠到的位置，使得．

（1）求证：平面平面；
（2）求证：平面．

（本小题满分12分）如图四棱锥，,,平面，，M为的中点．

（Ⅰ）求证：平面；
（Ⅱ）在平面上找一点N，使得平面；
（Ⅲ）求直线与平面所成角的正弦．

为等腰直角三角形，，，、分别是边和的中点，现将沿折起，使面面，、分别是边和的中点，平面与、分别交于、两点．

（Ⅰ）求证：；
（Ⅱ）求二面角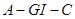的余弦值；

在四棱锥中，底面是边长为的菱形，，面，，，分别为，的中点．

（Ⅰ）求证：面；
（Ⅱ）求点到面的距离．

如图，在直三棱柱中，

（1）求证
（2）在上是否存在点使得
（3）在上是否存在点使得？

如图，在正方体中，、、分别是，，的中点．

（1）平面
（2）平面．

（本小题满分12分）如图，在三棱台中，分别为的中点．

（Ⅰ）求证：平面；
（Ⅱ）若平面，，，求平面与平面所成角（锐角）的大小．

如图1是边长为4的等边三角形，将其剪拼成一个正三棱柱模型（如图2），使它的全面积与原三角形的面积相等。D为AC上一点，且BDDC₁．

（1）求证：直线AB₁∥平面BDC₁
（2）求点A到平面BDC₁的距离．