如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.
(1)求证:平面A B1D1∥平面EFG;
(2)求 与平面
与平面 所成角的正切值
所成角的正切值
如图,在四棱锥 中,已知底面
中,已知底面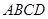 为矩形,
为矩形, 平面
平面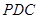 ,点
,点 为棱
为棱 的中点,求证:
的中点,求证:
(1) 平面
平面 ;
;
(2)平面 平面
平面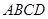 .
.
(本题9分)
在空间四边形ABCD中,CB=CD,AD⊥BD,点E、F分别是AB,BD的中点。
求证:
(1)直线EF∥平面ACD;
(2)平面EFC⊥平面BCD。
如图,四棱锥 的底面是矩形,侧面
的底面是矩形,侧面 是正三角形,且侧面
是正三角形,且侧面
 底面
底面 ,
, 为侧棱
为侧棱 的中点
的中点
(1)求证: //平面
//平面 ;
;
(2)求证: ⊥平面
⊥平面 ;
;
(3)若直线 与平面
与平面 所成的角为30
所成的角为30 ,求
,求 的值
的值
(本小题满分12分)
如图, 在三棱柱 中,
中,  底面
底面 ,
, ,
,  ,
, , 点D是
, 点D是 的中点.
的中点.
(Ⅰ) 求证 ; (Ⅱ) 求证
; (Ⅱ) 求证 ∥平面
∥平面 .
.
(本小题满分12分)已知如图,四边形 是直角梯形,
是直角梯形, ,
, ,
, 平面
平面 ,
, ,点
,点 、
、 、
、 分别是
分别是 、
、 、
、 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
 为等腰直角三角形,
为等腰直角三角形, ,
, ,
, 、
、 分别是边
分别是边 和
和 的中点,现将
的中点,现将 沿
沿 折起,使面
折起,使面
 面
面 ,
, 、
、 分别是边
分别是边 和
和 的中点,平面
的中点,平面 与
与 、
、 分别交于
分别交于 、
、 两点.
两点.
(Ⅰ)求证:

 ;
;
(Ⅱ)求二面角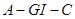 的余弦值;
的余弦值;
如图1是边长为4的等边三角形,将其剪拼成一个正三棱柱模型(如图2),使它的全面积与原三角形的面积相等。D为AC上一点,且BD DC1.
DC1.

(1)求证:直线AB1∥平面BDC1
(2)求点A到平面BDC1的距离.