如图，在四棱锥S﹣ABCD中，底面ABCD是正方形，其他四个侧面都是等边三角形，AC与BD的交点为O，E为侧棱SC上一点．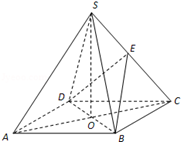
（Ⅰ）当E为侧棱SC的中点时，求证：SA∥平面BDE；
（Ⅱ）求证：平面BDE⊥平面SAC；
（Ⅲ）（理科）当二面角E﹣BD﹣C的大小为45°时，试判断点E在SC上的位置，并说明理由．
相关试题
中，直径
垂直于弦
，垂足为
，
是
切⊙
，连接
交
，证明：
的极值;
上是递增函数，求实数a的取值范围；
，求
.
;
.
，Z=18x推荐套卷
如图，在四棱锥S﹣ABCD中，底面ABCD是正方形，其他四个侧面都是等边三角形，AC与BD的交点为O，E为侧棱SC上一点．
（Ⅰ）当E为侧棱SC的中点时，求证：SA∥平面BDE；
（Ⅱ）求证：平面BDE⊥平面SAC；
（Ⅲ）（理科）当二面角E﹣BD﹣C的大小为45°时，试判断点E在SC上的位置，并说明理由．
粤公网安备 44130202000953号